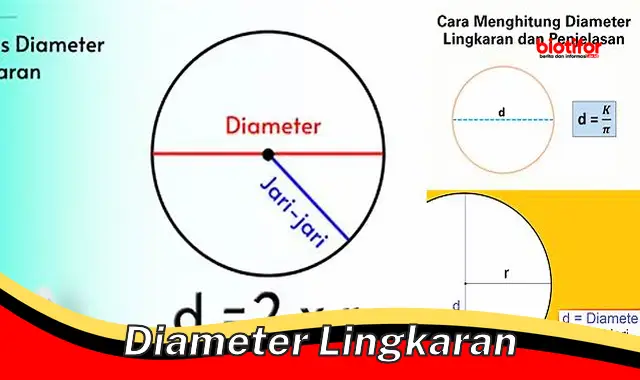
Diameter lingkaran adalah ruas garis yang menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran tersebut. Diameter merupakan jarak terpanjang dalam sebuah lingkaran, membagi lingkaran menjadi dua bagian yang sama besar.
Diameter lingkaran sangat penting dalam matematika dan fisika, serta memiliki beberapa sifat unik. Misalnya, diameter selalu lebih panjang dari jari-jari lingkaran, dan keliling lingkaran sama dengan kali diameternya.Diameter lingkaran juga memiliki sejarah panjang, dating kembali ke zaman Yunani kuno. Para matematikawan Yunani menggunakan diameter lingkaran untuk menghitung luas dan volume benda-benda bulat.
Dalam kehidupan sehari-hari, diameter lingkaran dapat ditemukan dalam berbagai aplikasi, seperti pada roda, bola, dan piringan. Diameter juga digunakan dalam teknik dan arsitektur untuk menentukan ukuran dan bentuk benda.
diameter lingkaran
Diameter lingkaran merupakan besaran penting yang terkait dengan bentuk dan ukuran lingkaran. Diameter memiliki beberapa aspek utama yang perlu dibahas, yaitu:
- Garis lurus
- Membagi dua lingkaran
- Memiliki nilai tetap
- Lebih panjang dari jari-jari
- Menghubungkan dua titik
- Sifat simetri
- Membentuk busur
- Digunakan dalam perhitungan
- Konsep dasar geometri
Kesepuluh aspek tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang diameter lingkaran. Diameter merupakan kunci untuk memahami sifat-sifat lingkaran, melakukan pengukuran dan perhitungan, serta mengaplikasikan konsep geometri dalam berbagai bidang ilmu dan kehidupan praktis.
Garis lurus
Dalam geometri, garis lurus merupakan konsep dasar yang merepresentasikan jarak terpendek antara dua titik. Garis lurus memiliki beberapa sifat unik, seperti tidak memiliki panjang, lebar, atau ketebalan, dan memanjang tak hingga ke dua arah.
-
Sebagai Diameter Lingkaran
Garis lurus menjadi diameter lingkaran ketika memenuhi dua syarat: menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran. Diameter merupakan jarak terpanjang dalam lingkaran dan membagi lingkaran menjadi dua bagian yang sama besar. -
Sifat Simetri
Diameter membagi lingkaran menjadi dua bagian yang simetris. Artinya, kedua bagian tersebut merupakan bayangan cermin satu sama lain. -
Membentuk Busur
Diameter dan kedua titik yang dihubungkannya pada lingkaran membentuk busur. Busur adalah bagian dari lingkaran yang dibatasi oleh dua titik tersebut. -
Pengukuran dan Perhitungan
Diameter lingkaran digunakan dalam berbagai pengukuran dan perhitungan. Misalnya, keliling lingkaran dapat dihitung dengan mengalikan diameter dengan (pi), dan luas lingkaran dihitung dengan mengalikan kuadrat diameter dengan (pi).
Konsep garis lurus dan diameter lingkaran saling terkait erat. Diameter merupakan jenis garis lurus khusus yang memiliki sifat dan peran penting dalam geometri, khususnya dalam konteks lingkaran.
Membagi dua lingkaran
Sifat diameter lingkaran yang sangat penting adalah kemampuannya membagi lingkaran menjadi dua bagian yang sama besar. Sifat ini memiliki beberapa implikasi dan signifikansi:
-
Definisi Diameter
Secara definisi, diameter adalah garis yang membagi dua sebuah lingkaran. Artinya, diameter membagi lingkaran menjadi dua bagian yang kongruen. -
Sifat Simetri
Pembagian lingkaran oleh diameter menghasilkan simetri. Kedua bagian lingkaran yang dibentuk oleh diameter merupakan bayangan cermin satu sama lain. -
Pengukuran dan Perhitungan
Sifat membagi dua lingkaran sangat penting dalam pengukuran dan perhitungan yang melibatkan lingkaran. Misalnya, untuk menentukan titik tengah lingkaran, kita dapat menarik diameter dan titik tengah akan terletak pada diameter tersebut. -
Aplikasi Praktis
Sifat membagi dua lingkaran memiliki banyak aplikasi praktis. Misalnya, dalam pembuatan roda, diameter roda menentukan ukuran dan bentuk roda, serta mempengaruhi stabilitas dan performa kendaraan.
Dengan demikian, sifat diameter lingkaran yang membagi dua lingkaran menjadi dua bagian yang sama besar merupakan aspek fundamental yang memberikan pemahaman mendalam tentang geometri lingkaran, serta memiliki berbagai aplikasi dalam kehidupan nyata.
Memiliki nilai tetap
Dalam konteks diameter lingkaran, “memiliki nilai tetap” mengacu pada sifat diameter yang selalu memiliki panjang yang sama untuk lingkaran tertentu. Sifat ini memiliki beberapa aspek penting:
-
Definisi Diameter
Diameter didefinisikan sebagai garis yang menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran. Sifat memiliki nilai tetap menunjukkan bahwa panjang diameter tidak berubah, terlepas dari posisi kedua titik yang dihubungkan pada lingkaran. -
Konstanta Lingkaran
Diameter merupakan konstanta atau besaran tetap untuk setiap lingkaran. Artinya, nilai diameter tidak bergantung pada ukuran atau bentuk lingkaran. Diameter selalu dua kali jari-jari lingkaran. -
Pengukuran dan Perhitungan
Sifat memiliki nilai tetap sangat penting dalam pengukuran dan perhitungan yang melibatkan lingkaran. Dengan mengetahui diameter, kita dapat dengan mudah menentukan keliling dan luas lingkaran menggunakan rumus yang sudah ditetapkan. -
Aplikasi Praktis
Sifat diameter yang memiliki nilai tetap memiliki banyak aplikasi praktis. Misalnya, dalam pembuatan roda, diameter roda harus memiliki nilai tertentu agar roda dapat berfungsi dengan baik. Dalam konstruksi, diameter pipa atau kabel harus sesuai dengan spesifikasi tertentu agar dapat menahan beban dengan aman.
Dengan demikian, sifat “memiliki nilai tetap” merupakan aspek penting dari diameter lingkaran yang memberikan pemahaman mendalam tentang geometri lingkaran dan memiliki berbagai aplikasi dalam kehidupan nyata.
Lebih panjang dari jari-jari
Dalam konteks diameter lingkaran, sifat “lebih panjang dari jari-jari” memiliki beberapa aspek penting:
-
Definisi Diameter dan Jari-jari
Diameter didefinisikan sebagai garis yang menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran, sedangkan jari-jari adalah ruas garis yang menghubungkan titik pada lingkaran dengan titik pusat. Sifat “lebih panjang dari jari-jari” menunjukkan bahwa panjang diameter lebih besar dari panjang jari-jari. -
Sifat Geometris
Secara geometris, diameter membagi lingkaran menjadi dua bagian yang sama besar. Sifat “lebih panjang dari jari-jari” menunjukkan bahwa garis bagi ini lebih panjang dari setiap ruas garis yang menghubungkan titik pada lingkaran dengan titik pusat (jari-jari). -
Pengukuran dan Perhitungan
Sifat “lebih panjang dari jari-jari” penting dalam pengukuran dan perhitungan yang melibatkan lingkaran. Diameter dan jari-jari terkait dengan rumus matematika tertentu, seperti keliling dan luas lingkaran. Mengetahui diameter memungkinkan kita menentukan jari-jari dan sebaliknya. -
Aplikasi Praktis
Sifat “lebih panjang dari jari-jari” memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam teknik, diameter poros atau pipa harus lebih panjang dari jari-jari untuk memastikan kekuatan dan stabilitas struktur.
Dengan demikian, sifat “lebih panjang dari jari-jari” adalah aspek penting dari diameter lingkaran yang memberikan pemahaman mendalam tentang geometri lingkaran dan memiliki berbagai aplikasi dalam kehidupan nyata.
Menghubungkan dua titik
Dalam konteks diameter lingkaran, sifat “menghubungkan dua titik” memiliki beberapa aspek penting:
-
Definisi Diameter
Diameter didefinisikan sebagai garis yang menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran. Sifat “menghubungkan dua titik” menunjukkan bahwa diameter merupakan garis bagi lingkaran, yang membagi lingkaran menjadi dua bagian yang sama besar. -
Sifat Geometris
Secara geometris, diameter merupakan garis terpanjang yang dapat digambar dalam suatu lingkaran. Sifat “menghubungkan dua titik” menunjukkan bahwa diameter menghubungkan dua titik terjauh pada lingkaran. -
Pengukuran dan Perhitungan
Sifat “menghubungkan dua titik” penting dalam pengukuran dan perhitungan yang melibatkan lingkaran. Dengan mengetahui diameter, kita dapat menentukan keliling dan luas lingkaran menggunakan rumus matematika tertentu. -
Aplikasi Praktis
Sifat “menghubungkan dua titik” memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam teknik, diameter poros atau pipa harus cukup panjang untuk menghubungkan dua titik tertentu dengan kuat dan stabil.
Dengan demikian, sifat “menghubungkan dua titik” merupakan aspek penting dari diameter lingkaran yang memberikan pemahaman mendalam tentang geometri lingkaran dan memiliki berbagai aplikasi dalam kehidupan nyata.
Sifat simetri
Sifat simetri merupakan salah satu aspek penting dari diameter lingkaran. Sifat ini berkaitan dengan pembagian lingkaran menjadi dua bagian yang sama besar oleh diameter. Pembagian ini menghasilkan simetri, baik secara bentuk maupun ukuran, pada kedua bagian lingkaran.
Sifat simetri diameter lingkaran memiliki beberapa implikasi penting. Pertama, simetri ini menjadi dasar bagi pengukuran dan perhitungan yang melibatkan lingkaran. Dengan mengetahui sifat simetri, kita dapat dengan mudah menentukan titik tengah, jari-jari, keliling, dan luas lingkaran.
Kedua, sifat simetri diameter lingkaran juga memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam arsitektur, simetri digunakan untuk menciptakan bangunan yang estetis dan seimbang. Dalam teknik, simetri digunakan untuk memastikan stabilitas dan kekuatan struktur. Dalam transportasi, simetri digunakan untuk merancang kendaraan yang efisien dan aerodinamis.
Dengan demikian, sifat simetri merupakan komponen penting dari diameter lingkaran yang memberikan pemahaman mendalam tentang sifat-sifat lingkaran dan memiliki berbagai aplikasi dalam kehidupan nyata.
Membentuk busur
Dalam konteks diameter lingkaran, sifat “membentuk busur” memiliki beberapa aspek penting yang terkait dengan pembagian lingkaran oleh diameter. Pembagian ini menghasilkan suatu busur, yang merupakan bagian dari lingkaran yang dibatasi oleh dua titik ujung diameter.
-
Busur Setengah Lingkaran
Diameter membagi lingkaran menjadi dua busur yang sama besar, yang disebut busur setengah lingkaran. Busur setengah lingkaran memiliki panjang yang sama dengan setengah keliling lingkaran.
-
Pembagian Busur
Diameter tidak hanya membagi lingkaran menjadi dua busur setengah lingkaran, tetapi juga membagi busur lainnya dalam lingkaran. Pembagian ini menghasilkan busur-busur yang lebih kecil dengan panjang yang berbeda.
-
Pengukuran Busur
Sifat “membentuk busur” penting dalam pengukuran dan perhitungan yang melibatkan lingkaran. Dengan mengetahui panjang diameter dan panjang busur, kita dapat menentukan keliling dan luas lingkaran menggunakan rumus matematika tertentu.
-
Aplikasi Praktis
Sifat “membentuk busur” memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam teknik, busur digunakan untuk membuat roda gigi, katrol, dan komponen mesin lainnya. Dalam arsitektur, busur digunakan untuk menciptakan lengkungan, kubah, dan struktur melengkung lainnya.
Secara keseluruhan, sifat “membentuk busur” merupakan komponen penting dari diameter lingkaran yang memberikan pemahaman mendalam tentang sifat-sifat lingkaran dan memiliki berbagai aplikasi dalam kehidupan nyata.
Digunakan dalam perhitungan
Diameter lingkaran memegang peran penting dalam berbagai perhitungan matematika, khususnya yang berkaitan dengan sifat-sifat lingkaran itu sendiri. Sifat-sifat ini mencakup keliling, luas, jari-jari, dan sudut pusat.
-
Keliling Lingkaran
Keliling lingkaran dihitung menggunakan rumus K = d, di mana K adalah keliling, adalah konstanta sekitar 3,14, dan d adalah diameter lingkaran. -
Luas Lingkaran
Luas lingkaran dihitung menggunakan rumus L = r2, di mana L adalah luas, adalah konstanta sekitar 3,14, dan r adalah jari-jari lingkaran. Karena diameter adalah dua kali jari-jari, maka rumus luas lingkaran juga dapat ditulis sebagai L = (d/2)2. -
Jari-jari Lingkaran
Jari-jari lingkaran dapat dihitung jika kita mengetahui diameternya. Rumus yang digunakan adalah r = d/2, di mana r adalah jari-jari dan d adalah diameter. -
Sudut Pusat Lingkaran
Sudut pusat lingkaran yang terbentuk oleh dua jari-jari yang ditarik dari titik pusat ke dua titik pada lingkaran dapat dihitung menggunakan rumus = (d/2r) x 180, di mana adalah sudut pusat, d adalah diameter, dan r adalah jari-jari.
Dengan demikian, diameter lingkaran merupakan besaran penting dalam perhitungan yang melibatkan lingkaran. Pemahaman tentang sifat-sifat diameter dan penggunaannya dalam perhitungan sangat penting dalam berbagai bidang, seperti matematika, fisika, teknik, dan arsitektur.
Konsep Dasar Geometri
Dalam geometri, diameter lingkaran merupakan konsep dasar yang memiliki peran penting dalam menentukan sifat-sifat lingkaran. Diameter berhubungan erat dengan konsep-konsep geometri lainnya, seperti jari-jari, keliling, luas, dan sudut pusat.
-
Panjang Garis
Diameter merupakan garis terpanjang dalam sebuah lingkaran yang menghubungkan dua titik terjauh pada lingkaran tersebut. Sifat ini menjadi dasar bagi pengukuran keliling dan luas lingkaran.
-
Pembagi Lingkaran
Diameter membagi lingkaran menjadi dua bagian yang sama besar, yang disebut setengah lingkaran. Sifat ini memudahkan dalam menentukan titik-titik penting pada lingkaran, seperti titik pusat dan jari-jari.
-
Konstanta Lingkaran
Diameter memiliki hubungan tetap dengan keliling dan luas lingkaran. Keliling lingkaran sama dengan kali diameter, sedangkan luas lingkaran sama dengan kali kuadrat diameter. Sifat ini menjadikan diameter sebagai besaran yang penting dalam perhitungan geometri.
-
Sudut Pusat
Diameter membentuk sudut pusat sebesar 180 derajat. Sifat ini berguna dalam menghitung besar sudut-sudut yang terbentuk oleh tali busur atau garis singgung pada lingkaran.
Dengan memahami konsep dasar geometri yang terkait dengan diameter lingkaran, kita dapat menganalisis dan menyelesaikan berbagai masalah geometri yang melibatkan lingkaran. Diameter menjadi kunci untuk menentukan sifat-sifat penting lingkaran dan melakukan perhitungan yang akurat.
Pertanyaan Umum tentang Diameter Lingkaran
Berikut adalah beberapa pertanyaan umum dan jawabannya mengenai diameter lingkaran untuk menambah pemahaman Anda:
Pertanyaan 1: Apa yang dimaksud dengan diameter lingkaran?
Diameter lingkaran adalah garis lurus yang menghubungkan dua titik pada lingkaran dan melalui titik pusat lingkaran. Diameter merupakan jarak terpanjang dalam sebuah lingkaran.
Pertanyaan 2: Mengapa diameter penting dalam geometri lingkaran?
Diameter memegang peranan penting karena membagi lingkaran menjadi dua bagian yang sama besar, sehingga memudahkan dalam menentukan sifat-sifat lingkaran seperti keliling, luas, dan sudut pusat.
Pertanyaan 3: Bagaimana cara mencari diameter lingkaran?
Untuk mencari diameter lingkaran, Anda dapat menggunakan rumus d = 2r, di mana d adalah diameter dan r adalah jari-jari lingkaran.
Pertanyaan 4: Apa hubungan antara diameter dan keliling lingkaran?
Keliling lingkaran sama dengan kali diameter. Dengan mengetahui diameter lingkaran, Anda dapat dengan mudah menentukan kelilingnya.
Pertanyaan 5: Apa saja aplikasi diameter lingkaran dalam kehidupan sehari-hari?
Diameter lingkaran memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti menentukan ukuran roda, menghitung luas permukaan benda berbentuk lingkaran, dan merancang struktur bangunan.
Pertanyaan 6: Mengapa diameter lingkaran selalu lebih panjang dari jari-jarinya?
Diameter selalu lebih panjang dari jari-jarinya karena diameter merupakan jarak terpanjang dalam sebuah lingkaran, sedangkan jari-jari adalah jarak dari titik pusat lingkaran ke titik pada lingkaran.
Dengan memahami diameter lingkaran dan sifat-sifatnya, Anda dapat menyelesaikan berbagai masalah geometri yang melibatkan lingkaran secara efektif.
Selanjutnya, kita akan membahas topik menarik lainnya yang berkaitan dengan lingkaran.
Tips untuk Memahami Diameter Lingkaran
Berikut adalah beberapa tips untuk membantu Anda memahami diameter lingkaran dengan lebih baik:
Tip 1: Pahami Definisi Dasar
Mulailah dengan memahami definisi diameter lingkaran, yaitu garis lurus yang menghubungkan dua titik pada lingkaran dan melalui titik pusatnya.
Tip 2: Hubungkan dengan Jari-jari
Ingatlah bahwa diameter adalah dua kali jari-jari lingkaran. Hubungan ini membantu Anda menentukan diameter jika jari-jarinya diketahui.
Tip 3: Gunakan Rumus
Gunakan rumus d = 2r untuk mencari diameter (d) jika jari-jari (r) diketahui. Rumus ini memudahkan perhitungan diameter.
Tip 4: Bagi Lingkaran
Pahami bahwa diameter membagi lingkaran menjadi dua bagian yang sama besar, yang disebut setengah lingkaran. Sifat ini membantu dalam menyelesaikan masalah terkait simetri dan pembagian lingkaran.
Tip 5: Terapkan pada Masalah Geometri
Terapkan konsep diameter lingkaran untuk menyelesaikan masalah geometri, seperti mencari keliling, luas, dan sudut pusat lingkaran. Diameter memainkan peran penting dalam perhitungan ini.
Tip 6: Visualisasikan
Gunakan gambar atau diagram untuk memvisualisasikan konsep diameter lingkaran. Representasi visual dapat meningkatkan pemahaman Anda.
Tip 7: Berlatih Soal
Berlatihlah mengerjakan soal-soal yang melibatkan diameter lingkaran. Latihan akan meningkatkan keterampilan Anda dalam menerapkan konsep ini.
Kesimpulan
Dengan mengikuti tips ini, Anda dapat membangun pemahaman yang kuat tentang diameter lingkaran. Konsep ini merupakan dasar penting dalam geometri dan memiliki berbagai aplikasi dalam kehidupan nyata.
Kesimpulan
Pembahasan mengenai diameter lingkaran memberikan pemahaman mendalam tentang konsep penting ini dalam geometri. Diameter merupakan garis terpanjang dalam sebuah lingkaran yang membagi lingkaran menjadi dua bagian yang sama besar dan memiliki peran krusial dalam menentukan sifat-sifat lingkaran, seperti keliling, luas, dan sudut pusat.
Memahami diameter lingkaran tidak hanya bermanfaat secara akademis, tetapi juga memiliki berbagai aplikasi praktis dalam bidang teknik, arsitektur, dan kehidupan sehari-hari. Dengan menguasai konsep ini, kita dapat menyelesaikan permasalahan geometri secara efektif dan memperoleh wawasan yang lebih luas tentang bentuk dan sifat-sifat lingkaran.
Youtube Video:
