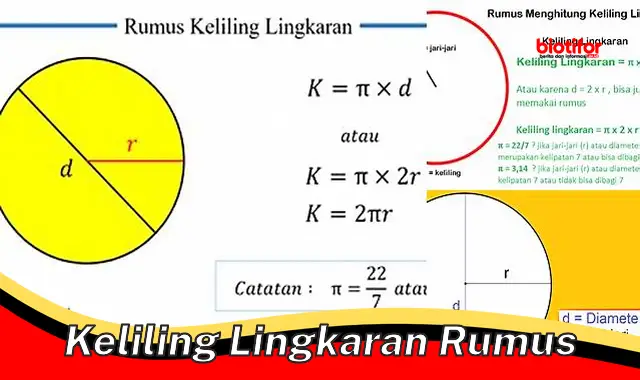
Keliling lingkaran adalah jarak di sekitar lingkaran. Rumus untuk keliling lingkaran adalah K = 2r, di mana K adalah keliling, adalah konstanta sekitar 3,14, dan r adalah jari-jari lingkaran. Kita dapat menggunakan rumus ini untuk menghitung keliling lingkaran apa pun jika kita mengetahui jari-jarinya.
Keliling lingkaran sangat penting dalam banyak bidang, seperti teknik, arsitektur, dan matematika. Ini digunakan untuk menghitung panjang pagar, keliling roda, dan banyak aplikasi lainnya. Memahami rumus keliling lingkaran memungkinkan kita untuk menyelesaikan masalah praktis dan mendesain struktur secara akurat.
Penemuan rumus keliling lingkaran telah ada sejak zaman kuno. Matematikawan Yunani Archimedes adalah salah satu orang pertama yang mengembangkan metode untuk menghitung keliling lingkaran. Sejak itu, rumus tersebut telah disempurnakan dan digunakan oleh banyak ilmuwan dan insinyur sepanjang sejarah.
Rumus Keliling Lingkaran
Rumus keliling lingkaran sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan matematika.
- Definisi: Jarak di sekitar lingkaran.
- Rumus: K = 2r, di mana K adalah keliling, adalah konstanta sekitar 3,14, dan r adalah jari-jari.
- Aplikasi: Menghitung panjang pagar, keliling roda, dan banyak lagi.
- Sejarah: Ditemukan oleh Archimedes pada zaman Yunani kuno.
- Ketepatan: Diperkirakan menggunakan pendekatan dan metode numerik.
- Keterbatasan: Hanya berlaku untuk lingkaran, bukan bentuk lainnya.
- Konstanta : Nilai irasional yang mewakili perbandingan keliling lingkaran dengan diameternya.
- Turunan: Dapat digunakan untuk menghitung luas lingkaran.
- Aplikasi Lanjutan: Digunakan dalam kalkulus, fisika, dan teknik mesin.
Memahami berbagai aspek rumus keliling lingkaran memungkinkan kita untuk menggunakannya secara efektif dalam berbagai aplikasi praktis. Dari menghitung panjang pagar hingga mendesain struktur yang efisien, rumus ini adalah alat penting yang telah membentuk dunia kita dengan berbagai cara.
Definisi
Definisi keliling lingkaran sebagai jarak di sekeliling lingkaran adalah dasar dari rumus keliling lingkaran. Rumus ini memungkinkan kita untuk menghitung keliling lingkaran jika kita mengetahui jari-jarinya. Tanpa definisi yang jelas tentang keliling lingkaran, kita tidak akan dapat mengembangkan rumus yang akurat untuk menghitungnya.
Sebagai contoh, dalam mendesain sebuah taman berbentuk lingkaran, kita perlu mengetahui kelilingnya untuk menentukan jumlah pagar yang dibutuhkan. Dengan menggunakan rumus keliling lingkaran, kita dapat menghitung keliling taman tersebut berdasarkan jari-jarinya, sehingga kita dapat merencanakan dan membangun pagar dengan tepat.
Pemahaman tentang definisi keliling lingkaran dan rumusnya sangat penting dalam berbagai bidang praktis, seperti teknik, arsitektur, dan matematika. Definisi ini memberikan dasar untuk menghitung dan mengukur keliling lingkaran, yang sangat penting untuk merancang dan membangun berbagai struktur dan objek.
Rumus
Rumus keliling lingkaran, K = 2r, adalah persamaan penting yang menghubungkan keliling lingkaran (K) dengan jari-jarinya (r). Konstanta (pi) adalah nilai irasional sekitar 3,14 yang mewakili perbandingan keliling lingkaran dengan diameternya. Rumus ini memungkinkan kita untuk menghitung keliling lingkaran jika kita mengetahui jari-jarinya, dan sebaliknya.
Sebagai bagian dari rumus keliling lingkaran secara keseluruhan, nilai memainkan peran penting. adalah konstanta matematika yang muncul di banyak persamaan dan rumus, dan merupakan bilangan irasional yang artinya tidak dapat dinyatakan sebagai pecahan dua bilangan bulat. Nilai telah dihitung hingga miliaran digit, dan merupakan salah satu konstanta paling terkenal dan penting dalam matematika.
Memahami hubungan antara rumus keliling lingkaran dan konstanta sangat penting untuk berbagai aplikasi praktis. Dalam teknik dan arsitektur, rumus ini digunakan untuk menghitung keliling roda, pipa, dan struktur melingkar lainnya. Dalam matematika, rumus ini digunakan untuk menghitung luas dan volume bangun ruang yang melibatkan lingkaran. Pemahaman yang baik tentang rumus keliling lingkaran dan nilai sangat penting untuk menyelesaikan masalah praktis dan mendesain struktur serta objek secara akurat.
Aplikasi
Rumus keliling lingkaran memiliki banyak aplikasi penting dalam kehidupan nyata, termasuk menghitung panjang pagar, keliling roda, dan banyak lagi. Pemahaman tentang rumus ini sangat penting untuk perhitungan akurat dalam berbagai bidang, seperti teknik, arsitektur, dan konstruksi.
Sebagai contoh, dalam membangun pagar di sekitar taman berbentuk lingkaran, kita perlu mengetahui keliling taman tersebut untuk menentukan jumlah pagar yang dibutuhkan. Dengan menggunakan rumus keliling lingkaran, kita dapat menghitung keliling taman berdasarkan jari-jarinya, sehingga kita dapat merencanakan dan membangun pagar dengan tepat. Kesalahan dalam menghitung keliling dapat menyebabkan kekurangan atau kelebihan pagar, yang dapat menimbulkan pemborosan biaya dan waktu.
Selain itu, rumus keliling lingkaran juga digunakan untuk menghitung keliling roda kendaraan. Keliling roda menentukan jarak yang ditempuh kendaraan untuk setiap putaran roda. Dengan mengetahui keliling roda, kita dapat menghitung jarak yang ditempuh kendaraan berdasarkan jumlah putaran roda, yang penting untuk mengukur jarak tempuh dan memantau kinerja kendaraan.
Memahami hubungan antara rumus keliling lingkaran dan aplikasinya sangat penting untuk berbagai profesi dan kegiatan. Rumus ini memungkinkan kita untuk menyelesaikan masalah praktis secara akurat, merancang struktur yang efisien, dan mengukur jarak dengan tepat. Pemahaman yang baik tentang rumus keliling lingkaran sangat penting untuk berbagai bidang, mulai dari teknik hingga fisika dan matematika.
Sejarah
Penemuan rumus keliling lingkaran oleh Archimedes pada zaman Yunani kuno merupakan tonggak penting dalam perkembangan matematika. Rumus ini telah menjadi dasar bagi banyak kemajuan dalam geometri, teknik, dan bidang lainnya selama berabad-abad.
-
Metode Pengukuran
Metode Archimedes untuk menghitung keliling lingkaran adalah dengan menggunakan poligon beraturan. Ia memulai dengan segitiga sama sisi yang tertulis dalam lingkaran, kemudian menggandakan jumlah sisi poligon untuk mendapatkan perkiraan keliling yang lebih akurat. Metode ini menunjukkan pemahaman mendalam tentang sifat-sifat lingkaran dan poligon. -
Nilai Pi
Melalui perhitungannya, Archimedes juga memperkirakan nilai (pi), konstanta penting yang digunakan dalam rumus keliling lingkaran. Perkiraannya sekitar 3,14, yang sangat dekat dengan nilai sebenarnya sekitar 3,14159. Penemuan memungkinkan perhitungan keliling lingkaran yang lebih akurat. -
Aplikasi Praktis
Rumus keliling lingkaran yang ditemukan oleh Archimedes memiliki banyak aplikasi praktis pada zaman kuno. Insinyur Yunani menggunakannya untuk mendesain roda kereta, bangunan, dan sistem irigasi. Pemahaman tentang keliling lingkaran sangat penting untuk merancang struktur yang kuat dan efisien.
Penemuan rumus keliling lingkaran oleh Archimedes merupakan bukti kecerdasan dan ketekunannya yang luar biasa. Rumus ini telah menjadi dasar bagi banyak kemajuan dalam matematika dan teknik, dan terus digunakan hingga saat ini untuk menyelesaikan masalah praktis dan mendesain struktur yang efisien.
Ketepatan
Ketepatan perhitungan keliling lingkaran sangat penting dalam berbagai aplikasi praktis. Pendekatan dan metode numerik digunakan untuk memperkirakan keliling lingkaran secara akurat, bahkan ketika nilai tidak diketahui atau sulit untuk dihitung secara pasti.
Salah satu metode numerik yang umum digunakan adalah metode Monte Carlo. Metode ini melibatkan pengambilan sejumlah titik acak di dalam lingkaran dan menggunakan rasio titik-titik yang berada di dalam lingkaran terhadap jumlah total titik untuk memperkirakan nilai . Metode ini memberikan perkiraan yang semakin akurat seiring dengan bertambahnya jumlah titik yang diambil.
Memahami ketepatan perhitungan keliling lingkaran sangat penting untuk memastikan hasil yang andal dan akurat. Dalam teknik dan arsitektur, perhitungan keliling lingkaran yang tepat sangat penting untuk merancang struktur yang kuat dan efisien. Dalam matematika, perhitungan keliling lingkaran yang akurat digunakan untuk menyelesaikan masalah geometri dan menghitung luas dan volume bangun ruang yang melibatkan lingkaran.
Dengan menggunakan pendekatan dan metode numerik, kita dapat memperkirakan keliling lingkaran dengan ketepatan yang tinggi, bahkan ketika nilai tidak diketahui atau sulit untuk dihitung secara pasti. Pemahaman tentang ketepatan perhitungan keliling lingkaran sangat penting untuk berbagai bidang, mulai dari teknik hingga fisika dan matematika.
Keterbatasan
Rumus keliling lingkaran hanya berlaku untuk bentuk lingkaran, tidak untuk bentuk lainnya. Hal ini merupakan keterbatasan penting untuk dipertimbangkan ketika menggunakan rumus ini untuk menyelesaikan masalah praktis. Untuk bentuk lain, seperti elips, persegi, atau segitiga, dibutuhkan rumus yang berbeda untuk menghitung kelilingnya.
Memahami keterbatasan ini sangat penting untuk memastikan penggunaan rumus keliling lingkaran secara tepat. Misalnya, dalam mendesain pagar di sekitar lapangan berbentuk persegi, kita tidak dapat menggunakan rumus keliling lingkaran karena lapangan tersebut bukan bentuk lingkaran. Kita perlu menggunakan rumus keliling persegi untuk mendapatkan hasil yang akurat.
Meskipun memiliki keterbatasan, rumus keliling lingkaran tetap menjadi alat yang sangat berguna untuk menyelesaikan masalah praktis yang melibatkan bentuk lingkaran. Dengan memahami keterbatasan ini dan menggunakan rumus yang tepat untuk bentuk yang berbeda, kita dapat menghitung keliling berbagai bentuk secara akurat, yang sangat penting dalam berbagai bidang seperti teknik, arsitektur, dan desain.
Konstanta
Konstanta (pi) adalah nilai irasional yang mewakili perbandingan keliling lingkaran dengan diameternya. Konstanta ini merupakan bilangan penting yang banyak digunakan dalam rumus keliling lingkaran, dan memiliki hubungan yang erat dengan konsep keliling lingkaran.
-
Sifat Bilangan Irasional
adalah bilangan irasional, yang berarti tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Sifat irasional ini membuat tidak dapat ditulis sebagai desimal yang berakhir atau berulang, dan memiliki digit yang tidak pernah berakhir. -
Perbandingan Keliling dan Diameter
Konstanta mewakili perbandingan keliling lingkaran dengan diameternya. Dengan kata lain, keliling lingkaran selalu sama dengan dikali diameternya. Hubungan ini sangat penting dalam menghitung keliling lingkaran, karena diameternya seringkali lebih mudah diukur dibandingkan kelilingnya. -
Aplikasi dalam Rumus Keliling Lingkaran
Konstanta digunakan dalam rumus keliling lingkaran, yaitu K = d, di mana K adalah keliling dan d adalah diameter. Rumus ini memungkinkan kita untuk menghitung keliling lingkaran dengan mudah dan akurat, sehingga sangat berguna dalam berbagai aplikasi, seperti teknik, arsitektur, dan desain. -
Konstanta Universal
Konstanta adalah konstanta universal yang berlaku untuk semua lingkaran. Artinya, nilai sama untuk semua lingkaran, terlepas dari ukuran atau bentuknya. Sifat universal ini membuat menjadi nilai yang sangat penting dan banyak digunakan dalam berbagai bidang.
Konstanta dan rumus keliling lingkaran memiliki hubungan yang erat dan saling melengkapi. Konstanta memberikan dasar matematis untuk menghitung keliling lingkaran, sedangkan rumus keliling lingkaran memungkinkan kita untuk menerapkan konsep ini dalam berbagai aplikasi praktis. Pemahaman tentang hubungan ini sangat penting untuk menggunakan rumus keliling lingkaran secara efektif dan menyelesaikan masalah yang melibatkan lingkaran.
Turunan
Turunan adalah konsep dalam kalkulus yang mengukur laju perubahan suatu fungsi. Dalam konteks keliling lingkaran, turunan dapat digunakan untuk menghitung luas lingkaran, yang merupakan besaran penting dalam geometri dan aplikasi praktis lainnya.
-
Menghitung Luas Lingkaran
Turunan dari fungsi keliling lingkaran terhadap jari-jarinya memberikan fungsi luas lingkaran. Dengan kata lain, dengan mengetahui turunan dari keliling lingkaran, kita dapat menghitung luas lingkaran dengan mudah dan akurat.
-
Aplikasi dalam Kalkulus
Konsep turunan dan hubungannya dengan luas lingkaran banyak digunakan dalam kalkulus. Misalnya, turunan dapat digunakan untuk menghitung volume bangun ruang yang melibatkan lingkaran, seperti kerucut dan bola.
-
Aplikasi dalam Fisika
Dalam fisika, turunan dan luas lingkaran digunakan untuk menghitung gaya dan tekanan yang bekerja pada benda berbentuk lingkaran, seperti roda dan pipa.
-
Aplikasi dalam Teknik
Di bidang teknik, turunan dan luas lingkaran digunakan untuk merancang dan menganalisis struktur yang melibatkan bentuk lingkaran, seperti jembatan dan bangunan.
Hubungan antara turunan dan keliling lingkaran sangat penting untuk memahami konsep luas lingkaran dan penerapannya dalam berbagai bidang. Dengan menggunakan turunan, kita dapat menghitung luas lingkaran dengan akurat dan menyelesaikan masalah praktis yang melibatkan bentuk lingkaran.
Aplikasi Lanjutan
Rumus keliling lingkaran tidak hanya terbatas pada aplikasi dasar seperti menghitung panjang pagar atau keliling roda, tetapi juga memiliki aplikasi lanjutan yang penting dalam berbagai bidang, termasuk kalkulus, fisika, dan teknik mesin.
Dalam kalkulus, turunan dari rumus keliling lingkaran digunakan untuk menghitung luas lingkaran. Konsep ini sangat penting dalam menghitung luas permukaan dan volume bangun ruang yang melibatkan bentuk lingkaran, seperti kerucut dan bola. Selain itu, turunan rumus keliling lingkaran juga digunakan untuk menentukan laju perubahan luas lingkaran terhadap jari-jarinya, yang berguna dalam analisis matematika.
Dalam fisika, rumus keliling lingkaran digunakan untuk menghitung gaya dan tekanan yang bekerja pada benda berbentuk lingkaran. Misalnya, rumus ini digunakan untuk menghitung tegangan pada roda yang berputar dan tekanan pada pipa melingkar. Pemahaman tentang rumus keliling lingkaran sangat penting untuk merancang dan menganalisis sistem fisik yang melibatkan gaya dan tekanan.
Dalam teknik mesin, rumus keliling lingkaran digunakan untuk merancang dan menganalisis komponen mesin yang melibatkan bentuk lingkaran, seperti roda gigi, poros, dan bantalan. Misalnya, rumus ini digunakan untuk menghitung gaya pada gigi roda gigi dan tegangan pada poros yang berputar. Pemahaman tentang rumus keliling lingkaran sangat penting untuk memastikan keamanan dan efisiensi komponen mesin.
Memahami aplikasi lanjutan dari rumus keliling lingkaran sangat penting dalam berbagai bidang teknik dan sains. Rumus ini menyediakan dasar matematis untuk menyelesaikan masalah kompleks yang melibatkan bentuk lingkaran, memungkinkan kita untuk merancang dan menganalisis struktur, mesin, dan sistem yang aman, efisien, dan dapat diandalkan.
Pertanyaan Umum tentang Rumus Keliling Lingkaran
Berikut adalah beberapa pertanyaan umum dan jawabannya tentang rumus keliling lingkaran:
Pertanyaan 1: Apa rumus keliling lingkaran?
Jawaban: Rumus keliling lingkaran adalah K = 2r, di mana K adalah keliling, adalah konstanta sekitar 3,14, dan r adalah jari-jari lingkaran.
Pertanyaan 2: Kapan rumus keliling lingkaran digunakan?
Jawaban: Rumus keliling lingkaran digunakan untuk menghitung keliling lingkaran, yaitu jarak di sekeliling lingkaran.
Pertanyaan 3: Apa itu (pi)?
Jawaban: (pi) adalah konstanta matematika sekitar 3,14 yang mewakili perbandingan keliling lingkaran dengan diameternya.
Pertanyaan 4: Bagaimana cara menghitung keliling lingkaran jika jari-jarinya diketahui?
Jawaban: Untuk menghitung keliling lingkaran jika jari-jarinya diketahui, gunakan rumus K = 2r, di mana r adalah jari-jari lingkaran.
Pertanyaan 5: Dalam bidang apa saja rumus keliling lingkaran digunakan?
Jawaban: Rumus keliling lingkaran digunakan dalam berbagai bidang, seperti teknik, arsitektur, matematika, fisika, dan teknik mesin.
Pertanyaan 6: Apa saja aplikasi praktis dari rumus keliling lingkaran?
Jawaban: Aplikasi praktis dari rumus keliling lingkaran antara lain menghitung panjang pagar, keliling roda, luas lingkaran, dan volume bangun ruang yang melibatkan lingkaran.
Memahami rumus keliling lingkaran dan aplikasinya sangat penting untuk berbagai bidang teknik, sains, dan kehidupan sehari-hari. Rumus ini memberikan dasar matematis untuk menyelesaikan masalah dan merancang struktur, mesin, dan sistem yang aman, efisien, dan dapat diandalkan.
Artikel Selanjutnya: Aplikasi Rumus Keliling Lingkaran dalam Teknik Mesin
Tips Menggunakan Rumus Keliling Lingkaran
Rumus keliling lingkaran, K = 2r, adalah alat penting yang digunakan dalam berbagai bidang. Untuk menggunakan rumus ini secara efektif, perhatikan beberapa tips berikut:
Tip 1: Pahami Konsep Jari-jari
Dalam rumus keliling lingkaran, huruf “r” mewakili jari-jari lingkaran. Jari-jari adalah jarak dari pusat lingkaran ke tepi lingkaran. Sangat penting untuk mengidentifikasi jari-jari dengan benar sebelum menggunakan rumus.
Tip 2: Konversi Satuan dengan Tepat
Konsistensi satuan sangat penting saat menggunakan rumus keliling lingkaran. Jika jari-jari diberikan dalam satuan sentimeter, maka keliling yang dihasilkan juga harus dalam satuan sentimeter. Konversi satuan yang tepat diperlukan untuk mendapatkan hasil yang akurat.
Tip 3: Gunakan Kalkulator yang Tepat
Nilai (pi) adalah konstanta sekitar 3,14. Menggunakan kalkulator yang memberikan nilai yang akurat sangat penting untuk memastikan hasil yang tepat. Hindari menggunakan kalkulator dasar yang mungkin membulatkan nilai , yang dapat menyebabkan kesalahan perhitungan.
Tip 4: Periksa Hasil Anda
Setelah menghitung keliling lingkaran, disarankan untuk memeriksa kembali hasil Anda. Anda dapat melakukan ini dengan mengukur keliling lingkaran secara langsung menggunakan pita pengukur atau dengan menggunakan metode alternatif untuk menghitung keliling lingkaran.
Tip 5: Terapkan dalam Praktik
Rumus keliling lingkaran memiliki berbagai aplikasi praktis. Anda dapat menggunakannya untuk menghitung panjang pagar, keliling roda, dan luas lingkaran. Memahami cara menerapkan rumus ini dalam situasi nyata akan meningkatkan keterampilan pemecahan masalah Anda.
Mengikuti tips ini akan membantu Anda menggunakan rumus keliling lingkaran secara efektif dan akurat. Rumus ini adalah alat yang berharga yang dapat digunakan untuk menyelesaikan berbagai masalah dalam berbagai bidang, mulai dari teknik hingga matematika.
Kesimpulan
Rumus keliling lingkaran, K = 2r, merupakan rumus penting yang digunakan dalam berbagai bidang teknik, arsitektur, dan matematika. Memahami rumus ini dan aplikasinya sangat penting untuk menyelesaikan masalah, merancang struktur, dan menganalisis sistem yang melibatkan bentuk lingkaran.Rumus keliling lingkaran memberikan dasar matematis untuk menghitung jarak di sekitar lingkaran, yang merupakan konsep mendasar dalam geometri. Aplikasi rumus ini sangat luas, mulai dari menghitung panjang pagar hingga menganalisis gaya pada roda yang berputar.Dengan memahami rumus keliling lingkaran dan penerapannya, kita dapat merancang dan membangun struktur, mesin, dan sistem yang aman, efisien, dan dapat diandalkan. Rumus ini adalah alat penting yang memungkinkan kita untuk memanfaatkan kekuatan matematika dalam memecahkan masalah dunia nyata yang melibatkan bentuk lingkaran.
Youtube Video:
