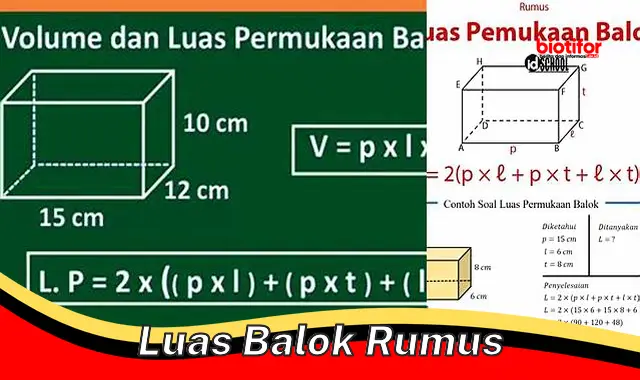
Luas balok rumus adalah sebuah rumus yang digunakan untuk menghitung luas permukaan balok. Rumus ini penting karena dapat digunakan untuk menghitung luas permukaan balok dengan cepat dan mudah.
Luas balok rumus memiliki beberapa manfaat, diantaranya:
- Menghemat waktu dan tenaga dalam menghitung luas permukaan balok.
- Memudahkan dalam mendesain dan membuat benda-benda yang berbentuk balok.
- Meningkatkan pemahaman tentang konsep luas permukaan balok.
Luas balok rumus memiliki sejarah yang panjang. Rumus ini pertama kali ditemukan oleh Archimedes pada abad ke-3 SM. Sejak saat itu, rumus ini telah digunakan secara luas dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Adapun topik-topik utama dalam luas balok rumus, antara lain:
- Pengertian luas permukaan balok.
- Rumus luas permukaan balok.
- Penerapan luas permukaan balok dalam kehidupan sehari-hari.
Luas Balok Rumus
Luas balok rumus merupakan aspek penting dalam matematika yang memiliki berbagai dimensi dan peran dalam kehidupan sehari-hari. Berikut adalah 10 aspek kunci terkait luas balok rumus:
- Pengertian luas permukaan balok
- Rumus luas permukaan balok
- Satuan luas permukaan balok
- Penerapan luas permukaan balok dalam kehidupan sehari-hari
- Jenis-jenis balok
- Sifat-sifat balok
- Sejarah luas permukaan balok
- Tokoh-tokoh yang berkontribusi pada pengembangan luas permukaan balok
- Perkembangan luas permukaan balok dalam matematika
- Masa depan luas permukaan balok
Kesepuluh aspek kunci tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang luas balok rumus. Misalnya, rumus luas permukaan balok tidak dapat dipahami tanpa terlebih dahulu memahami pengertian luas permukaan balok. Demikian pula, penerapan luas permukaan balok dalam kehidupan sehari-hari tidak dapat dibahas tanpa terlebih dahulu memahami jenis-jenis balok dan sifat-sifatnya. Dengan memahami aspek-aspek kunci ini, individu dapat memperoleh pemahaman yang lebih dalam tentang luas balok rumus dan perannya dalam berbagai bidang.
Pengertian Luas Permukaan Balok
Pengertian luas permukaan balok merupakan dasar untuk memahami luas balok rumus. Luas permukaan balok adalah jumlah luas semua sisi balok. Balok memiliki enam sisi, yaitu dua sisi alas, dua sisi samping, dan dua sisi atas bawah. Untuk menghitung luas permukaan balok, kita perlu mengetahui panjang, lebar, dan tinggi balok.
Luas balok rumus tidak dapat dipahami tanpa terlebih dahulu memahami pengertian luas permukaan balok. Hal ini dikarenakan rumus tersebut diturunkan dari pengertian luas permukaan balok. Dengan memahami pengertian luas permukaan balok, kita dapat dengan mudah memahami dan menerapkan rumus tersebut.
Contohnya, jika kita ingin menghitung luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm, maka kita dapat menggunakan rumus:
Luas permukaan balok = 2(panjang x lebar + panjang x tinggi + lebar x tinggi)
= 2(10 cm x 5 cm + 10 cm x 3 cm + 5 cm x 3 cm)
= 2(50 cm + 30 cm + 15 cm)
= 2(95 cm)
= 190 cm
Jadi, luas permukaan balok tersebut adalah 190 cm.
Memahami pengertian luas permukaan balok dan luas balok rumus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dengan memahami konsep-konsep ini, kita dapat menghitung luas permukaan balok dengan cepat dan mudah, sehingga dapat mengoptimalkan penggunaan bahan dan biaya.
Rumus Luas Permukaan Balok
Rumus luas permukaan balok adalah komponen penting dari luas balok rumus. Rumus ini digunakan untuk menghitung luas semua permukaan balok, yang terdiri dari dua sisi alas, dua sisi samping, dan dua sisi atas bawah. Memahami hubungan antara rumus luas permukaan balok dan luas balok rumus sangat penting untuk menghitung luas permukaan balok dengan cepat dan akurat.
Rumus luas permukaan balok diturunkan dari pengertian luas permukaan balok. Rumus tersebut menyatakan bahwa luas permukaan balok sama dengan dua kali jumlah luas alas, luas samping, dan luas atas bawah. Dengan menggunakan rumus ini, kita dapat menghitung luas permukaan balok dengan mudah jika kita mengetahui panjang, lebar, dan tinggi balok.
Contohnya, jika kita ingin menghitung luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm, maka kita dapat menggunakan rumus:
Luas permukaan balok = 2(panjang x lebar + panjang x tinggi + lebar x tinggi)
= 2(10 cm x 5 cm + 10 cm x 3 cm + 5 cm x 3 cm)
= 2(50 cm + 30 cm + 15 cm)
= 2(95 cm)
= 190 cm
Jadi, luas permukaan balok tersebut adalah 190 cm.
Memahami hubungan antara rumus luas permukaan balok dan luas balok rumus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dengan memahami konsep-konsep ini, kita dapat menghitung luas permukaan balok dengan cepat dan mudah, sehingga dapat mengoptimalkan penggunaan bahan dan biaya.
Satuan Luas Permukaan Balok
Satuan luas permukaan balok merupakan komponen penting dalam luas balok rumus. Satuan luas permukaan balok digunakan untuk menyatakan besaran luas permukaan balok. Tanpa adanya satuan, kita tidak dapat menentukan besarnya luas permukaan balok yang kita hitung.
Satuan luas permukaan balok yang umum digunakan adalah meter persegi (m2). Satuan ini digunakan untuk menyatakan luas permukaan balok dalam satuan meter. Misalnya, jika kita menghitung luas permukaan balok dan hasilnya adalah 10 m2, maka artinya luas permukaan balok tersebut adalah 10 meter persegi.
Selain meter persegi, terdapat juga satuan luas permukaan balok lainnya, seperti sentimeter persegi (cm2) dan milimeter persegi (mm2). Pemilihan satuan luas permukaan balok tergantung pada ukuran balok yang kita hitung. Untuk balok yang berukuran kecil, kita dapat menggunakan satuan sentimeter persegi atau milimeter persegi. Sedangkan untuk balok yang berukuran besar, kita dapat menggunakan satuan meter persegi.
Memahami hubungan antara satuan luas permukaan balok dan luas balok rumus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dengan memahami konsep-konsep ini, kita dapat menghitung luas permukaan balok dengan cepat dan akurat, sehingga dapat mengoptimalkan penggunaan bahan dan biaya.
Penerapan Luas Permukaan Balok dalam Kehidupan Sehari-hari
Penerapan luas permukaan balok dalam kehidupan sehari-hari sangatlah luas dan penting. Luas permukaan balok digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dalam arsitektur, luas permukaan balok digunakan untuk menghitung luas permukaan bangunan, seperti rumah, gedung, dan jembatan. Luas permukaan bangunan tersebut digunakan untuk menentukan kebutuhan bahan bangunan, seperti cat, plester, dan keramik.
Dalam teknik, luas permukaan balok digunakan untuk menghitung luas permukaan benda-benda, seperti mesin, kendaraan, dan pesawat terbang. Luas permukaan benda-benda tersebut digunakan untuk menentukan kebutuhan bahan bakar, efisiensi aerodinamis, dan kekuatan struktural.
Dalam desain, luas permukaan balok digunakan untuk menghitung luas permukaan produk, seperti kemasan, furnitur, dan peralatan rumah tangga. Luas permukaan produk tersebut digunakan untuk menentukan kebutuhan bahan baku, estetika produk, dan daya tahan produk.
Memahami hubungan antara penerapan luas permukaan balok dalam kehidupan sehari-hari dan luas balok rumus sangatlah penting. Dengan memahami konsep-konsep ini, kita dapat menghitung luas permukaan balok dengan cepat dan akurat, sehingga dapat mengoptimalkan penggunaan bahan, biaya, dan waktu.
Jenis-jenis Balok
Jenis-jenis balok memiliki kaitan erat dengan luas balok rumus. Pemahaman tentang jenis-jenis balok akan membantu dalam menentukan rumus yang tepat untuk menghitung luas permukaan balok. Terdapat beberapa jenis balok yang umum ditemukan, yaitu:
-
Balok Kubus
Balok kubus adalah balok yang memiliki panjang, lebar, dan tinggi yang sama. Rumus luas permukaan balok kubus adalah 6 x (sisi x sisi), dengan “sisi” mewakili panjang sisi kubus.
-
Balok Balok
Balok balok adalah balok yang memiliki panjang, lebar, dan tinggi yang berbeda. Rumus luas permukaan balok balok adalah 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)).
-
Balok Condong
Balok condong adalah balok yang memiliki alas dan tutup yang tidak sejajar. Rumus luas permukaan balok condong lebih kompleks dan memerlukan perhitungan tambahan untuk menentukan luas permukaan alas dan tutup yang tidak sejajar.
-
Balok Berongga
Balok berongga adalah balok yang memiliki rongga atau lubang di dalamnya. Rumus luas permukaan balok berongga dihitung dengan mengurangi luas permukaan rongga dari luas permukaan balok utuh.
Memahami jenis-jenis balok dan rumus yang sesuai untuk masing-masing jenis sangat penting dalam menghitung luas permukaan balok secara akurat. Dengan memahami konsep-konsep ini, kesalahan dalam perhitungan dapat diminimalkan dan hasil yang diperoleh akan lebih akurat.
Sifat-sifat Balok
Sifat-sifat balok memiliki kaitan yang erat dengan luas balok rumus. Sifat-sifat ini memengaruhi cara menghitung luas permukaan balok dan menentukan rumus yang tepat. Berikut adalah beberapa sifat balok yang penting terkait dengan luas balok rumus:
-
Memiliki enam sisi
Balok memiliki enam sisi, yaitu dua sisi alas, dua sisi samping, dan dua sisi atas bawah. Sifat ini memengaruhi rumus luas permukaan balok, yang melibatkan penjumlahan luas semua sisi tersebut.
-
Sisi-sisi yang sejajar sama luas
Dalam balok, sisi-sisi yang sejajar memiliki luas yang sama. Sifat ini menyederhanakan perhitungan luas permukaan balok karena luas sisi-sisi yang sejajar dapat dikalikan dengan dua.
-
Memiliki tiga ukuran: panjang, lebar, dan tinggi
Balok memiliki tiga ukuran, yaitu panjang, lebar, dan tinggi. Ketiga ukuran ini merupakan faktor penting dalam menentukan luas permukaan balok.
-
Bentuknya simetris
Balok memiliki bentuk yang simetris, artinya bentuknya sama jika dilihat dari sisi yang berbeda. Sifat ini membantu dalam memvisualisasikan balok dan menghitung luas permukaannya.
Memahami sifat-sifat balok dan hubungannya dengan luas balok rumus sangat penting untuk menghitung luas permukaan balok secara akurat. Dengan memahami konsep-konsep ini, kesalahan dalam perhitungan dapat diminimalkan dan hasil yang diperoleh akan lebih akurat.
Sejarah Luas Permukaan Balok
Sejarah luas permukaan balok tidak dapat dipisahkan dari perkembangan matematika itu sendiri. Konsep luas permukaan balok pertama kali ditemukan oleh para ahli matematika Yunani kuno, seperti Archimedes dan Euclid.
-
Masa Yunani Kuno
Pada masa Yunani kuno, Archimedes dan Euclid mengembangkan rumus untuk menghitung luas permukaan balok. Rumus ini didasarkan pada konsep luas segiempat dan luas lingkaran.
-
Masa Romawi Kuno
Pada masa Romawi kuno, Vitruvius mengembangkan rumus untuk menghitung volume balok. Rumus ini kemudian digunakan oleh para insinyur Romawi untuk membangun berbagai struktur, seperti kuil, jembatan, dan saluran air.
-
Masa Abad Pertengahan
Pada masa Abad Pertengahan, konsep luas permukaan balok terus berkembang. Para matematikawan Arab dan Persia mengembangkan rumus yang lebih akurat untuk menghitung luas permukaan balok.
-
Masa Renaisans
Pada masa Renaisans, konsep luas permukaan balok semakin disempurnakan. Para matematikawan Italia, seperti Leonardo da Vinci dan Luca Pacioli, mengembangkan rumus yang lebih umum untuk menghitung luas permukaan balok.
Rumus luas permukaan balok yang kita gunakan saat ini merupakan hasil dari perkembangan sejarah yang panjang. Rumus ini telah digunakan secara luas dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dengan memahami sejarah luas permukaan balok, kita dapat lebih menghargai pentingnya konsep ini dan kontribusi para matematikawan sepanjang sejarah.
Tokoh-tokoh yang berkontribusi pada pengembangan luas permukaan balok
Luas permukaan balok merupakan konsep penting dalam matematika yang memiliki banyak aplikasi dalam kehidupan nyata. Tokoh-tokoh bersejarah telah memberikan kontribusi signifikan pada pengembangan luas permukaan balok, yang mengarah pada pemahaman dan pemanfaatannya yang lebih baik.
Salah satu tokoh penting adalah Archimedes, matematikawan Yunani yang hidup pada abad ke-3 SM. Archimedes mengembangkan rumus untuk menghitung luas permukaan balok, yang masih digunakan hingga saat ini. Rumus ini didasarkan pada konsep luas persegi panjang dan luas lingkaran, dan memungkinkan kita untuk menghitung luas permukaan balok dengan cepat dan akurat.
Tokoh penting lainnya adalah Euclid, matematikawan Yunani yang juga hidup pada abad ke-3 SM. Euclid mengembangkan metode untuk menghitung volume balok, yang merupakan dasar dari rumus luas permukaan balok. Metode Euclid memungkinkan kita untuk menghitung volume balok dengan membagi balok menjadi prisma-prisma kecil yang lebih mudah untuk dihitung volumenya.
Selain Archimedes dan Euclid, banyak matematikawan lain yang telah berkontribusi pada pengembangan luas permukaan balok. Kontribusi mereka telah membantu kita untuk memahami konsep ini secara lebih mendalam dan menerapkannya dalam berbagai bidang.
Pemahaman tentang tokoh-tokoh yang berkontribusi pada pengembangan luas permukaan balok sangat penting karena memberikan kita apresiasi terhadap sejarah dan perkembangan matematika. Hal ini juga membantu kita untuk memahami pentingnya kerja sama dan kolaborasi dalam pengembangan pengetahuan ilmiah.
Perkembangan luas permukaan balok dalam matematika
Perkembangan luas permukaan balok dalam matematika memiliki hubungan yang sangat erat dengan luas balok rumus. Luas balok rumus merupakan rumus yang digunakan untuk menghitung luas permukaan balok, dan perkembangan luas permukaan balok dalam matematika telah membawa pada pengembangan rumus-rumus yang lebih akurat dan efisien.
Pada awalnya, rumus luas permukaan balok dikembangkan oleh matematikawan Yunani kuno seperti Archimedes dan Euclid. Rumus-rumus ini didasarkan pada konsep luas persegi panjang dan luas lingkaran, dan memungkinkan kita untuk menghitung luas permukaan balok dengan cepat dan akurat. Seiring waktu, matematikawan terus mengembangkan rumus-rumus yang lebih umum dan dapat diterapkan pada balok dengan bentuk yang lebih kompleks.
Perkembangan luas permukaan balok dalam matematika juga dipengaruhi oleh perkembangan kalkulus. Kalkulus memungkinkan kita untuk menghitung luas permukaan balok dengan lebih mudah dan efisien, bahkan untuk balok dengan bentuk yang sangat kompleks. Hal ini telah membuka jalan bagi penggunaan luas permukaan balok dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Pemahaman tentang perkembangan luas permukaan balok dalam matematika sangat penting karena memberikan kita apresiasi terhadap sejarah dan perkembangan matematika. Hal ini juga membantu kita untuk memahami pentingnya kerja sama dan kolaborasi dalam pengembangan pengetahuan ilmiah.
Masa Depan Luas Permukaan Balok
Masa depan luas permukaan balok sangat berkaitan erat dengan luas balok rumus. Dengan semakin berkembangnya teknologi dan ilmu pengetahuan, luas balok rumus akan terus dikembangkan agar dapat diterapkan pada masalah-masalah yang lebih kompleks dan menantang.
Salah satu perkembangan yang mungkin terjadi adalah penggunaan kecerdasan buatan (AI) dalam pengembangan luas balok rumus. AI dapat digunakan untuk mengotomatisasi proses perhitungan luas permukaan balok, sehingga dapat menghemat waktu dan tenaga.
Selain itu, luas balok rumus juga akan terus dikembangkan agar dapat diterapkan pada berbagai bidang baru. Misalnya, luas balok rumus dapat digunakan untuk mendesain material baru dengan sifat-sifat yang lebih unggul, atau untuk mengembangkan metode konstruksi baru yang lebih efisien dan ramah lingkungan.
Memahami hubungan antara masa depan luas permukaan balok dan luas balok rumus sangat penting karena memberikan kita wawasan tentang tren dan perkembangan terbaru dalam bidang matematika dan teknologinya. Hal ini juga membantu kita untuk memahami pentingnya luas balok rumus sebagai alat yang ampuh untuk memecahkan masalah-masalah di berbagai bidang.
Tanya Jawab Seputar Luas Balok Rumus
Berikut adalah beberapa pertanyaan umum dan jawabannya seputar luas balok rumus:
Pertanyaan 1: Apa itu luas balok rumus?
Jawaban: Luas balok rumus adalah rumus yang digunakan untuk menghitung luas permukaan balok. Rumus ini digunakan untuk menentukan jumlah seluruh luas sisi-sisi balok.
Pertanyaan 2: Bagaimana cara menggunakan luas balok rumus?
Jawaban: Untuk menggunakan luas balok rumus, diperlukan mengetahui panjang, lebar, dan tinggi balok. Rumus yang digunakan adalah 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)).
Pertanyaan 3: Dalam bidang apa saja luas balok rumus digunakan?
Jawaban: Luas balok rumus digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, desain interior, dan pengemasan.
Pertanyaan 4: Apakah ada jenis-jenis balok yang berbeda?
Jawaban: Ya, terdapat beberapa jenis balok, seperti balok kubus, balok balok, balok condong, dan balok berongga. Masing-masing jenis balok memiliki rumus luas permukaan yang berbeda.
Pertanyaan 5: Bagaimana cara menghitung luas permukaan balok tidak beraturan?
Jawaban: Untuk menghitung luas permukaan balok tidak beraturan, perlu membagi balok menjadi beberapa bangun ruang yang lebih sederhana, seperti balok, prisma, atau limas. Kemudian, hitung luas permukaan masing-masing bangun ruang dan jumlahkan hasilnya.
Pertanyaan 6: Apa manfaat mempelajari luas balok rumus?
Jawaban: Mempelajari luas balok rumus bermanfaat untuk memahami konsep luas permukaan, menghitung kebutuhan material bangunan, mendesain produk kemasan, dan menyelesaikan soal-soal matematika.
Dengan memahami pertanyaan dan jawaban di atas, diharapkan dapat membantu pemahaman mengenai luas balok rumus secara lebih komprehensif.
Catatan: Pertanyaan dan jawaban di atas dapat disesuaikan dengan kebutuhan dan target audiens yang spesifik.
Tips Menggunakan Luas Balok Rumus
Berikut adalah beberapa tips untuk menggunakan luas balok rumus secara efektif:
Tip 1: Pahami Konsep Luas Permukaan Balok
Sebelum menggunakan rumus, pastikan terlebih dahulu memahami konsep luas permukaan balok. Luas permukaan balok adalah jumlah seluruh luas sisi-sisi balok.
Tip 2: Identifikasi Jenis Balok
Terdapat beberapa jenis balok, seperti balok kubus, balok balok, balok condong, dan balok berongga. Masing-masing jenis balok memiliki rumus luas permukaan yang berbeda. Pastikan untuk mengidentifikasi jenis balok yang akan dihitung luas permukaannya.
Tip 3: Gunakan Rumus yang Tepat
Gunakan rumus yang sesuai dengan jenis balok yang akan dihitung. Misalnya, untuk balok balok, rumus yang digunakan adalah 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)).
Tip 4: Satuan yang Konsisten
Pastikan untuk menggunakan satuan yang konsisten saat menggunakan rumus. Misalnya, jika panjang, lebar, dan tinggi balok dalam satuan sentimeter, maka luas permukaan yang dihasilkan juga dalam satuan sentimeter persegi.
Tip 5: Periksa Hasil Perhitungan
Setelah menghitung luas permukaan balok, periksa kembali hasilnya untuk memastikan tidak ada kesalahan perhitungan. Salah satu cara untuk memeriksa adalah dengan menggunakan rumus luas permukaan balok yang berbeda.
Dengan mengikuti tips-tips di atas, Anda dapat menggunakan luas balok rumus secara lebih efektif dan akurat.
Kesimpulan:
Luas balok rumus merupakan alat yang sangat berguna untuk menghitung luas permukaan balok. Dengan memahami konsep luas permukaan balok, mengidentifikasi jenis balok, menggunakan rumus yang tepat, menjaga konsistensi satuan, dan memeriksa hasil perhitungan, Anda dapat menggunakan luas balok rumus secara efektif untuk berbagai keperluan.
Kesimpulan
Luas balok rumus merupakan konsep penting dalam matematika yang memiliki banyak aplikasi praktis dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain industri. Rumus ini memungkinkan kita untuk menghitung luas permukaan balok dengan mudah dan akurat, sehingga dapat menghemat waktu dan tenaga.
Dengan memahami luas balok rumus secara mendalam, kita dapat menyelesaikan berbagai permasalahan terkait luas permukaan balok secara efektif. Konsep ini menjadi dasar bagi pengembangan ilmu pengetahuan dan teknologi di masa depan, sehingga penting untuk dipelajari dan dipahami dengan baik.
Youtube Video:
