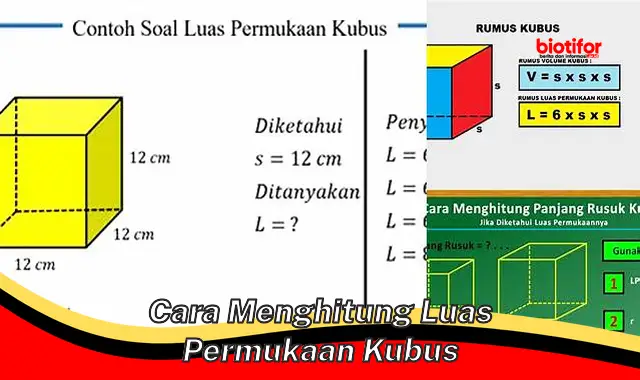
Luas permukaan kubus adalah jumlah luas semua sisi kubus. Untuk menghitung luas permukaan kubus, kita perlu mengalikan luas salah satu sisinya dengan 6. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaan kubusnya adalah 6 x (5 cm x 5 cm) = 150 cm2.
Luas permukaan kubus penting karena dapat digunakan untuk menghitung volume kubus, serta untuk menghitung luas bidang miring pada kubus. Mengetahui cara menghitung luas permukaan kubus juga penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Untuk menghitung luas permukaan kubus, kita dapat menggunakan rumus berikut:
- Luas permukaan kubus = 6 x (sisi x sisi)
di mana:
- sisi adalah panjang salah satu sisi kubus
Cara Menghitung Luas Permukaan Kubus
Luas permukaan kubus merupakan besaran penting yang sering digunakan dalam berbagai bidang, seperti matematika, fisika, dan teknik. Berikut adalah 8 aspek penting terkait cara menghitung luas permukaan kubus:
- Definisi: Luas permukaan kubus adalah jumlah luas semua sisi kubus.
- Rumus: Luas permukaan kubus = 6 x (sisi x sisi), di mana sisi adalah panjang salah satu sisi kubus.
- Satuan: Satuan luas permukaan kubus adalah satuan luas, seperti cm2, m2, atau km2.
- Aplikasi: Luas permukaan kubus digunakan untuk menghitung volume kubus dan luas bidang miring pada kubus.
- Contoh: Jika kubus memiliki sisi sepanjang 5 cm, maka luas permukaan kubusnya adalah 6 x (5 cm x 5 cm) = 150 cm2.
- Hubungan dengan bangun ruang lainnya: Luas permukaan kubus berhubungan dengan luas permukaan balok dan prisma.
- Sejarah: Konsep luas permukaan kubus telah dikenal sejak zaman kuno, digunakan oleh para ahli matematika seperti Euclid dan Archimedes.
- Perkembangan: Rumus luas permukaan kubus telah dikembangkan dan disempurnakan selama berabad-abad, dan saat ini menjadi konsep dasar dalam geometri.
Dengan memahami aspek-aspek penting ini, kita dapat menghitung luas permukaan kubus secara akurat dan menerapkannya dalam berbagai bidang yang membutuhkannya.
Definisi
Definisi luas permukaan kubus sangat penting dalam memahami cara menghitung luas permukaan kubus. Definisi ini menjelaskan bahwa luas permukaan kubus merupakan total luas dari semua sisi penyusun kubus tersebut.
-
Komponen Luas Permukaan Kubus
Luas permukaan kubus terdiri dari luas keenam sisinya. Setiap sisi kubus berbentuk persegi, sehingga luas setiap sisi dapat dihitung dengan mengalikan panjang sisinya dengan lebar sisinya. -
Contoh Penerapan
Misalnya, jika sebuah kubus memiliki panjang sisi 5 cm, maka luas permukaan kubus tersebut adalah jumlah luas keenam sisinya, yaitu 6 x (5 cm x 5 cm) = 150 cm2. -
Implikasi dalam Cara Menghitung Luas Permukaan Kubus
Definisi luas permukaan kubus menjadi dasar dalam menghitung luas permukaan kubus. Dengan mengetahui definisi ini, kita dapat menggunakan rumus luas permukaan kubus, yaitu Luas permukaan kubus = 6 x (sisi x sisi), untuk menghitung luas permukaan kubus.
Dengan memahami definisi luas permukaan kubus, kita dapat memahami konsep dasar dalam menghitung luas permukaan kubus dan menerapkan rumus yang tepat untuk menyelesaikan masalah yang terkait dengan luas permukaan kubus.
Rumus
Rumus luas permukaan kubus merupakan komponen penting dalam memahami cara menghitung luas permukaan kubus. Rumus ini memberikan langkah-langkah jelas untuk menghitung luas permukaan kubus, menjadikannya alat yang sangat penting dalam geometri.
Rumus ini menunjukkan bahwa luas permukaan kubus bergantung pada panjang sisi kubus. Dengan mengetahui panjang sisi, kita dapat dengan mudah menghitung luas permukaan kubus menggunakan rumus ini. Rumus ini berlaku untuk semua jenis kubus, terlepas dari ukuran atau orientasinya.
Dalam prakteknya, rumus ini banyak digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Misalnya, arsitek menggunakan rumus ini untuk menghitung luas permukaan bangunan berbentuk kubus, sementara insinyur menggunakannya untuk menghitung luas permukaan tangki berbentuk kubus. Pemahaman tentang rumus ini sangat penting untuk melakukan perhitungan yang akurat dalam berbagai bidang tersebut.
Dengan memahami rumus luas permukaan kubus, kita dapat menghitung luas permukaan kubus secara efisien dan akurat. Rumus ini menjadi dasar dalam memahami cara menghitung luas permukaan kubus dan menyelesaikan masalah yang terkait dengan luas permukaan kubus.
Satuan
Satuan luas permukaan kubus sangat penting dalam “cara menghitung luas permukaan kubus” karena menunjukkan hasil pengukuran luas permukaan kubus. Satuan luas ini memastikan bahwa hasil perhitungan luas permukaan kubus dapat diinterpretasikan dan dibandingkan dengan benar.
Satuan luas permukaan kubus yang umum digunakan adalah sentimeter persegi (cm2), meter persegi (m2), dan kilometer persegi (km2). Pemilihan satuan luas yang tepat bergantung pada ukuran kubus yang diukur. Misalnya, jika sebuah kubus memiliki sisi sepanjang beberapa sentimeter, maka satuan luas yang sesuai untuk menghitung luas permukaannya adalah sentimeter persegi (cm2). Namun, jika sebuah kubus memiliki sisi sepanjang beberapa meter, maka satuan luas yang sesuai adalah meter persegi (m2).
Memahami satuan luas permukaan kubus sangat penting untuk menghindari kesalahan dalam perhitungan. Jika satuan luas yang digunakan tidak sesuai, maka hasil perhitungan luas permukaan kubus akan salah dan dapat menyebabkan kesimpulan yang keliru. Oleh karena itu, penting untuk selalu memperhatikan satuan luas yang digunakan saat menghitung luas permukaan kubus agar diperoleh hasil yang akurat dan bermakna.
Aplikasi
Luas permukaan kubus memiliki keterkaitan yang erat dengan “cara menghitung luas permukaan kubus”, karena luas permukaan kubus merupakan dasar untuk menghitung volume kubus dan luas bidang miring pada kubus.
-
Menghitung Volume Kubus
Volume kubus dapat dihitung menggunakan rumus Volume = (sisi x sisi x sisi). Rumus ini diturunkan dari konsep luas permukaan kubus, di mana volume kubus dapat dihitung dengan mengalikan luas permukaan kubus dengan tinggi kubus. -
Menghitung Luas Bidang Miring pada Kubus
Luas bidang miring pada kubus dapat dihitung menggunakan rumus Luas bidang miring = (2/4) x (sisi x sisi). Rumus ini diturunkan dari konsep luas permukaan kubus, di mana luas bidang miring merupakan setengah dari luas permukaan kubus.
Dengan memahami keterkaitan antara luas permukaan kubus, volume kubus, dan luas bidang miring pada kubus, kita dapat menghitung besaran-besaran tersebut secara akurat. Hal ini penting dalam berbagai bidang aplikasi, seperti arsitektur, teknik, dan matematika.
Contoh
Contoh yang diberikan merupakan ilustrasi langsung dari “cara menghitung luas permukaan kubus” dan menyoroti aspek-aspek penting berikut:
-
Penerapan Rumus
Contoh ini menunjukkan penerapan rumus luas permukaan kubus, yaitu Luas permukaan kubus = 6 x (sisi x sisi), untuk menghitung luas permukaan kubus dengan sisi tertentu. -
Penentuan Sisi Kubus
Contoh ini menekankan bahwa luas permukaan kubus bergantung pada panjang sisinya. Dengan mengetahui panjang sisinya, seperti yang diberikan dalam contoh (5 cm), kita dapat menghitung luas permukaan kubus. -
Hasil Perhitungan
Contoh ini memberikan hasil perhitungan luas permukaan kubus, yaitu 150 cm2. Hasil ini menunjukkan luas permukaan kubus dengan sisi sepanjang 5 cm.
Dengan memahami contoh ini, kita dapat melihat bagaimana “cara menghitung luas permukaan kubus” diterapkan dalam praktik untuk menghitung luas permukaan kubus dengan panjang sisi tertentu. Contoh ini juga menekankan hubungan antara panjang sisi kubus dan luas permukaannya, serta pentingnya menggunakan rumus yang benar untuk perhitungan yang akurat.
Hubungan dengan bangun ruang lainnya
Hubungan antara luas permukaan kubus dengan luas permukaan balok dan prisma sangat penting dalam “cara menghitung luas permukaan kubus” karena memungkinkan kita untuk menghitung luas permukaan kubus menggunakan rumus luas permukaan balok atau prisma. Hal ini berguna ketika kita memiliki kubus yang tidak beraturan atau memiliki bentuk yang dimodifikasi, sehingga sulit untuk menghitung luas permukaannya secara langsung.
Misalnya, jika kita memiliki sebuah balok dengan panjang 5 cm, lebar 3 cm, dan tinggi 2 cm, maka luas permukaan balok tersebut dapat dihitung menggunakan rumus Luas permukaan balok = 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi)). Dengan memasukkan nilai-nilai yang diberikan, kita memperoleh luas permukaan balok = 2 x ((5 cm x 3 cm) + (5 cm x 2 cm) + (3 cm x 2 cm)) = 60 cm2.
Namun, jika kita memiliki sebuah kubus dengan sisi sepanjang 5 cm, maka luas permukaan kubusnya dapat dihitung dengan menggunakan rumus Luas permukaan kubus = 6 x (sisi x sisi), yang menghasilkan luas permukaan kubus = 6 x (5 cm x 5 cm) = 150 cm2. Kita dapat melihat bahwa luas permukaan kubus sama dengan luas permukaan balok dengan panjang 5 cm, lebar 5 cm, dan tinggi 5 cm.
Dengan memahami hubungan antara luas permukaan kubus dengan luas permukaan balok dan prisma, kita dapat menghitung luas permukaan kubus menggunakan rumus yang lebih mudah dan sesuai dengan bentuk kubus yang sebenarnya.
Sejarah
Konsep luas permukaan kubus telah dikenal sejak zaman kuno, dan para ahli matematika seperti Euclid dan Archimedes telah menggunakan konsep ini untuk menghitung volume dan luas permukaan kubus. Konsep ini sangat penting dalam “cara menghitung luas permukaan kubus” karena memberikan dasar teoretis dan historis untuk metode perhitungan yang digunakan saat ini.
Euclid, seorang ahli matematika Yunani yang hidup pada abad ke-3 SM, menulis sebuah buku berjudul “Elements” yang berisi dasar-dasar geometri. Dalam buku ini, Euclid mendefinisikan luas permukaan kubus sebagai jumlah luas semua sisinya, dan ia memberikan rumus untuk menghitung luas permukaan kubus, yaitu Luas permukaan kubus = 6 x (sisi x sisi). Rumus ini masih digunakan hingga saat ini untuk menghitung luas permukaan kubus.
Archimedes, seorang ahli matematika Yunani yang hidup pada abad ke-3 SM, juga memberikan kontribusi yang signifikan terhadap perkembangan konsep luas permukaan kubus. Archimedes menemukan bahwa luas permukaan kubus berbanding lurus dengan kuadrat sisinya. Penemuan ini sangat penting karena memungkinkan untuk menghitung luas permukaan kubus tanpa harus menghitung luas masing-masing sisinya.
Dengan memahami sejarah konsep luas permukaan kubus, kita dapat lebih menghargai metode perhitungan yang digunakan saat ini dan pentingnya konsep ini dalam matematika dan sains.
Perkembangan
Perkembangan rumus luas permukaan kubus sangat erat kaitannya dengan “cara menghitung luas permukaan kubus”, karena rumus tersebut merupakan dasar untuk menghitung luas permukaan kubus. Selama berabad-abad, para ahli matematika telah mengembangkan dan menyempurnakan rumus ini, menjadikannya konsep dasar dalam geometri yang digunakan secara luas hingga saat ini.
-
Penyempurnaan Rumus
Dari masa Euclid hingga Archimedes, rumus luas permukaan kubus terus disempurnakan untuk meningkatkan akurasi dan keefektifannya. Penyempurnaan ini mencakup pengembangan rumus yang lebih umum dan aplicable untuk berbagai bentuk kubus. -
Penerapan Praktis
Seiring dengan perkembangan rumus, penerapan praktisnya juga terus berkembang. Rumus luas permukaan kubus digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan desain, untuk menghitung luas permukaan bangunan, tangki, dan objek tiga dimensi lainnya. -
Dasar Pembelajaran Geometri
Rumus luas permukaan kubus menjadi konsep dasar dalam pembelajaran geometri. Rumus ini diajarkan di sekolah-sekolah dan menjadi dasar untuk memahami konsep luas permukaan bangun ruang lainnya. -
Kontribusi Tokoh Matematika
Tokoh-tokoh matematika seperti Euclid, Archimedes, dan Rene Descartes memberikan kontribusi signifikan dalam pengembangan rumus luas permukaan kubus. Kontribusi mereka membantu menyempurnakan rumus dan memperluas penerapannya.
Dengan memahami perkembangan rumus luas permukaan kubus, kita dapat mengapresiasi pentingnya konsep ini dalam “cara menghitung luas permukaan kubus” dan penggunaannya yang luas dalam berbagai bidang. Perkembangan ini juga menunjukkan bagaimana matematika terus berkembang dan disempurnakan untuk memecahkan masalah dan memenuhi kebutuhan manusia.
Pertanyaan Umum tentang Cara Menghitung Luas Permukaan Kubus
Untuk memberikan pemahaman yang komprehensif tentang cara menghitung luas permukaan kubus, berikut adalah beberapa pertanyaan umum yang sering diajukan:
Pertanyaan 1: Apa yang dimaksud dengan luas permukaan kubus?
Luas permukaan kubus adalah jumlah luas dari semua sisi kubus.
Pertanyaan 2: Bagaimana rumus untuk menghitung luas permukaan kubus?
Luas permukaan kubus = 6 x (sisi x sisi), dimana sisi adalah panjang salah satu sisi kubus.
Pertanyaan 3: Satuan apa yang digunakan untuk menyatakan luas permukaan kubus?
Satuan luas, seperti cm2, m2, atau km2.
Pertanyaan 4: Apa saja aplikasi dari luas permukaan kubus?
Menghitung volume kubus dan luas bidang miring pada kubus.
Pertanyaan 5: Bagaimana hubungan luas permukaan kubus dengan bangun ruang lainnya?
Luas permukaan kubus berhubungan dengan luas permukaan balok dan prisma.
Pertanyaan 6: Bagaimana sejarah perkembangan rumus luas permukaan kubus?
Konsep luas permukaan kubus telah dikenal sejak zaman kuno, dengan kontribusi dari ahli matematika seperti Euclid dan Archimedes.
Dengan memahami pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih baik tentang cara menghitung luas permukaan kubus dan penerapannya dalam berbagai bidang.
Transisi ke bagian artikel berikutnya:
Tips Menghitung Luas Permukaan Kubus
Untuk memperoleh hasil perhitungan luas permukaan kubus yang akurat dan efisien, berikut adalah beberapa tips yang dapat diterapkan:
Tips 1: Pahami Konsep Luas Permukaan Kubus
Sebelum menghitung luas permukaan kubus, penting untuk memahami konsepnya terlebih dahulu. Luas permukaan kubus merupakan jumlah luas dari seluruh sisi kubus. Dengan memahami konsep ini, akan lebih mudah untuk mengidentifikasi sisi-sisi kubus dan menghitung luas masing-masing sisi.
Tips 2: Tentukan Panjang Sisi Kubus
Untuk menghitung luas permukaan kubus menggunakan rumus, diperlukan nilai panjang sisi kubus. Pastikan untuk mengukur atau memperoleh nilai panjang sisi kubus dengan akurat. Ketidakakuratan dalam menentukan panjang sisi akan berdampak pada hasil perhitungan luas permukaan kubus.
Tips 3: Gunakan Rumus yang Tepat
Luas permukaan kubus dihitung menggunakan rumus khusus, yaitu Luas permukaan kubus = 6 x (sisi x sisi). Pastikan untuk menggunakan rumus yang tepat dan memasukkan nilai panjang sisi dengan benar. Hindari kesalahan dalam penggunaan rumus atau perhitungan.
Tips 4: Perhatikan Satuan
Hasil perhitungan luas permukaan kubus harus dinyatakan dalam satuan luas yang sesuai, seperti sentimeter persegi (cm2), meter persegi (m2), atau kilometer persegi (km2). Perhatikan satuan yang digunakan dalam soal atau yang diminta dalam perhitungan.
Tips 5: Lakukan Pengecekan
Setelah menghitung luas permukaan kubus, lakukan pengecekan ulang untuk memastikan hasilnya masuk akal. Bandingkan hasil dengan perkiraan atau gunakan metode lain untuk memverifikasi kebenaran hasil perhitungan.
Dengan mengikuti tips ini, diharapkan dapat membantu memperoleh hasil perhitungan luas permukaan kubus yang akurat dan efisien.
Kesimpulan:
Kesimpulan
Cara menghitung luas permukaan kubus merupakan konsep penting dalam geometri dan memiliki berbagai aplikasi praktis. Dengan memahami definisi, rumus, dan prinsip-prinsip yang mendasarinya, individu dapat menghitung luas permukaan kubus secara akurat dan efisien.
Pengetahuan tentang cara menghitung luas permukaan kubus berkontribusi pada pemahaman yang lebih komprehensif tentang bangun ruang dan hubungannya dengan konsep matematika lainnya. Selain itu, hal ini membekali individu dengan keterampilan yang berharga untuk memecahkan masalah dalam bidang-bidang seperti arsitektur, teknik, dan desain.
Youtube Video:
