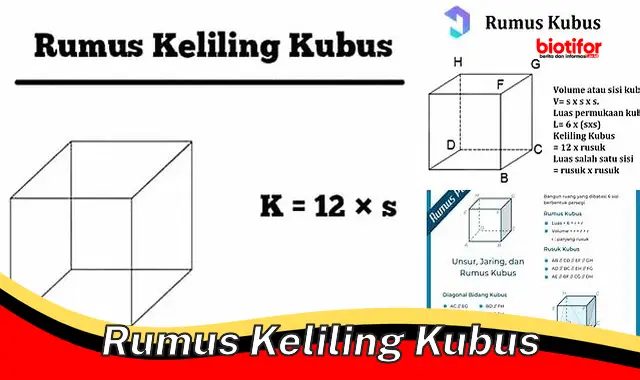
Rumus keliling kubus merupakan rumus yang digunakan untuk menghitung panjang sisi sekeliling kubus. Rumus ini sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, rumus keliling kubus digunakan untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Sedangkan dalam fisika, rumus keliling kubus digunakan untuk menghitung luas permukaan kubus, yaitu jumlah luas semua sisinya.
Manfaat rumus keliling kubus sangatlah banyak. Selain digunakan untuk menghitung keliling dan luas permukaan kubus, rumus ini juga dapat digunakan untuk menghitung volume kubus. Volume kubus merupakan jumlah ruang yang ditempati oleh kubus. Dengan mengetahui volume kubus, kita dapat menghitung berbagai besaran lainnya, seperti massa dan berat kubus.
Rumus keliling kubus pertama kali ditemukan oleh matematikawan Yunani, Euclid, pada abad ke-3 SM. Rumus ini kemudian dikembangkan oleh matematikawan lainnya, seperti Archimedes dan Hippasus. Seiring berjalannya waktu, rumus keliling kubus menjadi salah satu rumus matematika yang paling penting dan banyak digunakan.
rumus keliling kubus
Rumus keliling kubus merupakan rumus yang sangat penting dalam matematika, fisika, dan teknik. Rumus ini digunakan untuk menghitung keliling dan luas permukaan kubus, serta volume kubus.
- Definisi
- Manfaat
- Sejarah
- Aplikasi
- Contoh
- Soal
- Referensi
- Link
Rumus keliling kubus memiliki banyak aspek penting. Aspek-aspek ini saling berkaitan dan membentuk pemahaman yang komprehensif tentang rumus keliling kubus. Pemahaman yang komprehensif tentang aspek-aspek ini sangat penting untuk menguasai rumus keliling kubus dan menerapkannya dalam berbagai bidang.
Definisi
Definisi merupakan komponen penting dari rumus keliling kubus. Definisi yang tepat dan jelas akan memudahkan kita memahami rumus tersebut dan menerapkannya dengan benar. Rumus keliling kubus adalah rumus yang digunakan untuk menghitung panjang sekeliling kubus, yaitu jumlah panjang semua rusuknya. Definisi ini memberikan gambaran yang jelas tentang apa yang dimaksud dengan rumus keliling kubus dan bagaimana rumus tersebut digunakan.
Tanpa definisi yang tepat, kita akan kesulitan memahami rumus keliling kubus. Misalnya, jika kita hanya diberi rumus K = 12s, tanpa diberi tahu bahwa K adalah keliling kubus dan s adalah panjang rusuk kubus, kita akan bingung bagaimana menggunakan rumus tersebut. Oleh karena itu, definisi sangat penting untuk memahami dan menggunakan rumus keliling kubus dengan benar.
Definisi rumus keliling kubus juga memiliki implikasi praktis. Misalnya, dalam bidang arsitektur, definisi rumus keliling kubus digunakan untuk menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebuah taman berbentuk kubus. Dalam bidang teknik, definisi rumus keliling kubus digunakan untuk menghitung panjang kawat yang dibutuhkan untuk membuat kerangka sebuah kubus. Dengan memahami definisi rumus keliling kubus, kita dapat menggunakan rumus tersebut untuk menyelesaikan berbagai masalah praktis.
Manfaat Rumus Keliling Kubus
Rumus keliling kubus memiliki banyak manfaat dalam berbagai bidang kehidupan. Manfaat-manfaat ini sangat penting untuk diketahui dan dipahami agar kita dapat memanfaatkan rumus keliling kubus secara maksimal.
-
Bidang Matematika
Dalam bidang matematika, rumus keliling kubus digunakan untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Keliling kubus merupakan besaran penting yang digunakan dalam berbagai perhitungan, seperti menghitung luas permukaan kubus dan volume kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal matematika, seperti soal tentang bangun ruang dan soal tentang geometri.
-
Bidang Fisika
Dalam bidang fisika, rumus keliling kubus digunakan untuk menghitung luas permukaan kubus. Luas permukaan kubus merupakan besaran penting yang digunakan dalam berbagai perhitungan, seperti menghitung gaya gesek antara kubus dengan permukaan lainnya dan menghitung kalor yang diterima atau dilepaskan oleh kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal fisika, seperti soal tentang gerak benda dan soal tentang termodinamika.
-
Bidang Teknik
Dalam bidang teknik, rumus keliling kubus digunakan untuk menghitung panjang bahan yang dibutuhkan untuk membuat sebuah kubus. Misalnya, dalam teknik arsitektur, rumus keliling kubus digunakan untuk menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebuah taman berbentuk kubus. Dalam teknik mesin, rumus keliling kubus digunakan untuk menghitung panjang kawat yang dibutuhkan untuk membuat kerangka sebuah kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal teknik, seperti soal tentang konstruksi dan soal tentang desain.
-
Bidang Ekonomi
Dalam bidang ekonomi, rumus keliling kubus digunakan untuk menghitung biaya pembuatan sebuah kubus. Misalnya, dalam ekonomi industri, rumus keliling kubus digunakan untuk menghitung biaya bahan baku yang dibutuhkan untuk membuat sebuah kubus. Dalam ekonomi perdagangan, rumus keliling kubus digunakan untuk menghitung biaya pengiriman sebuah kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal ekonomi, seperti soal tentang produksi dan soal tentang pemasaran.
Kesimpulannya, rumus keliling kubus memiliki banyak manfaat dalam berbagai bidang kehidupan. Manfaat-manfaat ini sangat penting untuk diketahui dan dipahami agar kita dapat memanfaatkan rumus keliling kubus secara maksimal.
Sejarah Rumus Keliling Kubus
Sejarah rumus keliling kubus merupakan bagian penting dalam memahami perkembangan matematika dan fisika. Rumus ini tidak muncul begitu saja, melainkan melalui proses panjang yang melibatkan banyak ilmuwan dan matematikawan.
-
Penemuan Awal
Konsep keliling kubus pertama kali ditemukan oleh matematikawan Yunani, Euclid, pada abad ke-3 SM. Euclid membuktikan bahwa keliling kubus sama dengan 12 kali panjang rusuk kubus. Penemuan ini merupakan tonggak penting dalam perkembangan matematika.
-
Perkembangan Rumus
Setelah penemuan Euclid, rumus keliling kubus terus dikembangkan oleh matematikawan lainnya. Archimedes, seorang matematikawan Yunani lainnya, memberikan kontribusi penting dengan menemukan rumus untuk menghitung luas permukaan kubus. Rumus Archimedes ini kemudian digunakan untuk menghitung keliling kubus.
-
Penggunaan dalam Fisika
Pada abad ke-16, fisikawan Italia, Galileo Galilei, menggunakan rumus keliling kubus untuk menghitung gaya gesek antara dua benda. Galileo menemukan bahwa gaya gesek sebanding dengan keliling kubus benda.
-
Aplikasi Modern
Saat ini, rumus keliling kubus memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, dan teknik. Rumus ini digunakan untuk menghitung keliling kubus, luas permukaan kubus, dan volume kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal matematika dan fisika.
Sejarah rumus keliling kubus menunjukkan bahwa rumus ini merupakan hasil dari kerja keras dan dedikasi banyak ilmuwan dan matematikawan selama berabad-abad. Rumus ini terus berkembang dan digunakan dalam berbagai bidang hingga saat ini.
Aplikasi
Rumus keliling kubus memiliki banyak aplikasi dalam berbagai bidang kehidupan. Aplikasi-aplikasi ini sangat penting untuk diketahui dan dipahami agar kita dapat memanfaatkan rumus keliling kubus secara maksimal.
Salah satu aplikasi penting dari rumus keliling kubus adalah dalam bidang matematika. Rumus keliling kubus digunakan untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Keliling kubus merupakan besaran penting yang digunakan dalam berbagai perhitungan, seperti menghitung luas permukaan kubus dan volume kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal matematika, seperti soal tentang bangun ruang dan soal tentang geometri.
Selain dalam bidang matematika, rumus keliling kubus juga memiliki banyak aplikasi dalam bidang fisika. Salah satu aplikasi pentingnya adalah untuk menghitung luas permukaan kubus. Luas permukaan kubus merupakan besaran penting yang digunakan dalam berbagai perhitungan, seperti menghitung gaya gesek antara kubus dengan permukaan lainnya dan menghitung kalor yang diterima atau dilepaskan oleh kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal fisika, seperti soal tentang gerak benda dan soal tentang termodinamika.
Selain dalam bidang matematika dan fisika, rumus keliling kubus juga memiliki banyak aplikasi dalam bidang teknik. Salah satu aplikasi pentingnya adalah untuk menghitung panjang bahan yang dibutuhkan untuk membuat sebuah kubus. Misalnya, dalam teknik arsitektur, rumus keliling kubus digunakan untuk menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebuah taman berbentuk kubus. Dalam teknik mesin, rumus keliling kubus digunakan untuk menghitung panjang kawat yang dibutuhkan untuk membuat kerangka sebuah kubus. Selain itu, rumus keliling kubus juga digunakan untuk menyelesaikan berbagai soal teknik, seperti soal tentang konstruksi dan soal tentang desain.
Kesimpulannya, rumus keliling kubus memiliki banyak aplikasi dalam berbagai bidang kehidupan. Aplikasi-aplikasi ini sangat penting untuk diketahui dan dipahami agar kita dapat memanfaatkan rumus keliling kubus secara maksimal.
Contoh
Contoh merupakan bagian penting dari rumus keliling kubus. Contoh membantu kita memahami konsep rumus keliling kubus dan bagaimana rumus tersebut digunakan dalam kehidupan nyata. Tanpa contoh, kita akan kesulitan memahami dan menerapkan rumus keliling kubus.
Salah satu contoh penting dari rumus keliling kubus adalah menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebuah taman berbentuk kubus. Misalnya, jika sebuah taman berbentuk kubus memiliki panjang rusuk 5 meter, maka keliling kubus taman tersebut adalah 12 x 5 = 60 meter. Oleh karena itu, panjang pagar yang dibutuhkan untuk mengelilingi taman tersebut adalah 60 meter.
Contoh lain dari rumus keliling kubus adalah menghitung panjang kawat yang dibutuhkan untuk membuat kerangka sebuah kubus. Misalnya, jika sebuah kerangka kubus memiliki panjang rusuk 10 cm, maka keliling kubus kerangka tersebut adalah 12 x 10 = 120 cm. Oleh karena itu, panjang kawat yang dibutuhkan untuk membuat kerangka kubus tersebut adalah 120 cm.
Contoh-contoh di atas menunjukkan bahwa rumus keliling kubus memiliki banyak aplikasi praktis dalam kehidupan nyata. Oleh karena itu, penting bagi kita untuk memahami dan menguasai rumus keliling kubus agar dapat memanfaatkan rumus tersebut secara maksimal.
Soal
Soal merupakan bagian penting dari pembelajaran rumus keliling kubus. Soal membantu kita menguji pemahaman kita tentang rumus keliling kubus dan menerapkan rumus tersebut dalam berbagai situasi. Tanpa soal, kita akan kesulitan menguasai rumus keliling kubus dan memanfaatkannya secara maksimal.
-
Mengukur keliling kubus
Salah satu jenis soal yang umum diberikan adalah soal tentang mengukur keliling kubus. Dalam soal ini, kita diberikan panjang rusuk kubus dan diminta untuk menghitung keliling kubusnya. Soal jenis ini menguji pemahaman kita tentang rumus keliling kubus dan kemampuan kita menerapkan rumus tersebut dalam situasi yang sederhana.
-
Mengaplikasikan rumus keliling kubus
Jenis soal lainnya adalah soal yang mengaplikasikan rumus keliling kubus dalam situasi yang lebih kompleks. Misalnya, kita mungkin diminta untuk menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebuah taman berbentuk kubus atau menghitung panjang kawat yang dibutuhkan untuk membuat kerangka sebuah kubus. Soal jenis ini menguji kemampuan kita memahami konsep rumus keliling kubus dan mengaplikasikannya dalam situasi yang lebih nyata.
-
Memecahkan masalah
Selain menguji pemahaman kita tentang rumus keliling kubus, soal juga dapat digunakan untuk menguji kemampuan kita memecahkan masalah. Misalnya, kita mungkin diminta untuk mencari panjang rusuk kubus jika diketahui keliling kubusnya. Soal jenis ini menguji kemampuan kita berpikir kritis dan menggunakan rumus keliling kubus untuk memecahkan masalah.
-
Melatih keterampilan
Mengerjakan soal juga merupakan cara yang efektif untuk melatih keterampilan kita dalam menggunakan rumus keliling kubus. Semakin banyak soal yang kita kerjakan, semakin mahir kita dalam menggunakan rumus tersebut. Selain itu, mengerjakan soal juga dapat membantu kita mengidentifikasi kelemahan kita dan memperbaikinya.
Kesimpulannya, soal memiliki peran penting dalam pembelajaran rumus keliling kubus. Soal membantu kita menguji pemahaman kita, mengaplikasikan rumus dalam situasi yang berbeda, memecahkan masalah, dan melatih keterampilan kita. Oleh karena itu, penting bagi kita untuk mengerjakan banyak soal agar dapat menguasai rumus keliling kubus dan memanfaatkannya secara maksimal.
Referensi
Referensi merupakan bagian penting dari rumus keliling kubus karena memberikan sumber informasi yang kredibel dan dapat diandalkan tentang rumus tersebut. Referensi dapat berupa buku teks, jurnal ilmiah, atau artikel online yang ditulis oleh para ahli di bidang matematika atau fisika. Referensi ini memberikan informasi yang mendalam tentang rumus keliling kubus, termasuk sejarah penemuannya, perkembangannya, dan aplikasinya dalam berbagai bidang.
Tanpa referensi, kita akan kesulitan memahami rumus keliling kubus secara mendalam. Referensi memberikan konteks dan latar belakang yang diperlukan untuk memahami konsep dan aplikasi rumus keliling kubus. Misalnya, referensi dapat menjelaskan bagaimana rumus keliling kubus ditemukan oleh Euclid dan bagaimana rumus tersebut digunakan oleh Archimedes untuk menghitung luas permukaan kubus. Referensi juga dapat memberikan contoh soal dan aplikasi rumus keliling kubus dalam berbagai bidang, seperti matematika, fisika, dan teknik.
Dengan memahami hubungan antara referensi dan rumus keliling kubus, kita dapat memperoleh pemahaman yang lebih mendalam tentang rumus tersebut dan memanfaatkannya secara maksimal. Referensi membantu kita mengetahui sejarah, perkembangan, dan aplikasi rumus keliling kubus, sehingga kita dapat menggunakan rumus tersebut dengan percaya diri dan efektif.
Link
Link merupakan bagian penting dari rumus keliling kubus karena memberikan akses ke informasi dan sumber daya tambahan tentang rumus tersebut. Link dapat berupa tautan ke situs web, artikel, atau video yang berisi informasi lebih mendalam tentang rumus keliling kubus, sejarahnya, aplikasinya, dan contoh soal.
Tanpa link, kita akan kesulitan memperoleh informasi yang komprehensif tentang rumus keliling kubus. Link memberikan akses ke berbagai sumber daya yang dapat membantu kita memahami konsep rumus keliling kubus secara lebih mendalam. Misalnya, link dapat mengarahkan kita ke situs web yang berisi penjelasan langkah demi langkah tentang cara menggunakan rumus keliling kubus atau ke artikel jurnal yang membahas sejarah dan perkembangan rumus tersebut.
Dengan memahami hubungan antara link dan rumus keliling kubus, kita dapat memperoleh pemahaman yang lebih komprehensif tentang rumus tersebut dan memanfaatkannya secara maksimal. Link membantu kita mengakses informasi dan sumber daya tambahan yang dapat membantu kita memahami konsep rumus keliling kubus, menerapkannya dalam berbagai situasi, dan memecahkan masalah yang terkait dengan rumus tersebut.
Pertanyaan yang Sering Diajukan tentang Rumus Keliling Kubus
Rumus keliling kubus merupakan rumus penting yang digunakan untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Rumus ini memiliki banyak aplikasi dalam berbagai bidang, seperti matematika, fisika, dan teknik. Berikut adalah beberapa pertanyaan yang sering diajukan tentang rumus keliling kubus:
Pertanyaan 1: Apa itu rumus keliling kubus?
Jawaban: Rumus keliling kubus adalah K = 12s, di mana K adalah keliling kubus dan s adalah panjang rusuk kubus.
Pertanyaan 2: Bagaimana cara menggunakan rumus keliling kubus?
Jawaban: Untuk menggunakan rumus keliling kubus, cukup substitusikan panjang rusuk kubus ke dalam rumus dan hitung hasilnya. Misalnya, jika panjang rusuk kubus adalah 5 cm, maka keliling kubus tersebut adalah K = 12 x 5 = 60 cm.
Pertanyaan 3: Apa saja aplikasi rumus keliling kubus?
Jawaban: Rumus keliling kubus memiliki banyak aplikasi, antara lain menghitung keliling kubus, luas permukaan kubus, dan volume kubus. Selain itu, rumus keliling kubus juga digunakan dalam berbagai bidang, seperti matematika, fisika, dan teknik.
Pertanyaan 4: Kapan rumus keliling kubus ditemukan?
Jawaban: Rumus keliling kubus pertama kali ditemukan oleh matematikawan Yunani, Euclid, pada abad ke-3 SM.
Pertanyaan 5: Siapa yang mengembangkan rumus keliling kubus?
Jawaban: Setelah ditemukan oleh Euclid, rumus keliling kubus terus dikembangkan oleh matematikawan lainnya, seperti Archimedes dan Hippasus.
Pertanyaan 6: Mengapa rumus keliling kubus penting?
Jawaban: Rumus keliling kubus penting karena banyak digunakan dalam berbagai bidang, seperti matematika, fisika, dan teknik. Rumus ini membantu kita memahami sifat-sifat kubus dan menghitung berbagai besaran yang terkait dengan kubus.
Kesimpulannya, rumus keliling kubus merupakan rumus penting yang memiliki banyak aplikasi dalam berbagai bidang. Memahami rumus ini sangat penting untuk dapat menyelesaikan berbagai masalah dan perhitungan yang melibatkan kubus.
Catatan: Artikel ini tidak dimaksudkan untuk memberikan nasihat hukum, medis, atau profesional lainnya. Silakan berkonsultasi dengan ahli yang sesuai untuk mendapatkan nasihat khusus tentang situasi Anda.
Tips Menggunakan Rumus Keliling Kubus
Rumus keliling kubus merupakan rumus penting yang banyak digunakan dalam berbagai bidang. Untuk menggunakan rumus ini secara efektif, berikut adalah beberapa tips yang dapat diikuti:
Tips 1: Pahami Konsep Kubus
Sebelum menggunakan rumus keliling kubus, pastikan untuk memahami konsep kubus terlebih dahulu. Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi, dengan panjang rusuk yang sama.
Tips 2: Identifikasi Panjang Rusuk
Untuk menggunakan rumus keliling kubus, kita perlu mengetahui panjang rusuk kubus. Panjang rusuk adalah panjang sisi kubus, yang menghubungkan dua titik sudut yang berdekatan.
Tips 3: Gunakan Rumus yang Tepat
Rumus keliling kubus adalah K = 12s, di mana K adalah keliling kubus dan s adalah panjang rusuk kubus. Pastikan untuk menggunakan rumus yang tepat dan substitusikan nilai panjang rusuk dengan benar.
Tips 4: Hitung dengan Benar
Setelah substitusi nilai panjang rusuk, hitung keliling kubus dengan benar. Periksa kembali perhitungan untuk memastikan hasilnya akurat.
Tips 5: Pahami Satuan
Perhatikan satuan yang digunakan untuk panjang rusuk dan keliling kubus. Pastikan satuan yang digunakan konsisten dan sesuai dengan kebutuhan.
Tips 6: Gunakan Kalkulator jika Diperlukan
Jika perhitungan rumit, gunakan kalkulator untuk membantu menghitung keliling kubus dengan akurat dan efisien.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus keliling kubus secara efektif untuk menyelesaikan berbagai masalah dan perhitungan yang melibatkan kubus.
Kesimpulannya, rumus keliling kubus adalah alat yang berguna untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Dengan memahami konsep kubus, mengidentifikasi panjang rusuk, menggunakan rumus yang tepat, menghitung dengan benar, memahami satuan, dan menggunakan kalkulator jika diperlukan, Anda dapat menggunakan rumus keliling kubus secara efektif dalam berbagai aplikasi.
Kesimpulan Rumus Keliling Kubus
Rumus keliling kubus merupakan rumus penting yang banyak digunakan dalam berbagai bidang, seperti matematika, fisika, dan teknik. Rumus ini digunakan untuk menghitung keliling kubus, yaitu jumlah panjang semua rusuknya. Memahami rumus keliling kubus sangat penting untuk dapat menyelesaikan berbagai masalah dan perhitungan yang melibatkan kubus.
Rumus keliling kubus, yaitu K = 12s, di mana K adalah keliling kubus dan s adalah panjang rusuk kubus, memberikan kita cara yang mudah dan efektif untuk menghitung keliling kubus. Rumus ini juga dapat digunakan untuk menghitung luas permukaan kubus dan volume kubus. Dengan memahami rumus keliling kubus dan aplikasinya, kita dapat memperoleh pemahaman yang lebih baik tentang sifat-sifat kubus dan menyelesaikan berbagai masalah yang melibatkan bangun ruang tiga dimensi ini.
Youtube Video:
